Question

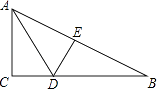
【题目】如图，在△ABC中，AB=AC，AD是角平分线，BE平分∠ABC交AD于点E，点O在AB上，以OB为半径的⊙O经过点E，交AB于点F．

（1）求证：AD是⊙O的切线；

（2）若AC=4，∠C=30°，求的长．

Answer 1

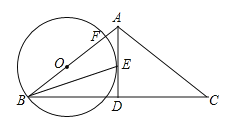
【答案】（1）证明见解析；（2）．

【解析】

试题分析：（1）连接OE，利用角平分线的定义和圆的性质可得∠OBE=∠OEB=∠EBD，可证明OE∥BD，结合等腰三角形的性质可得AD⊥BD，可证得OE⊥AD，可证得AD为切线；

（2）利用（1）的结论，结合条件可求得∠AOE=30°，由AC的长可求得圆的半径，利用弧长公式可求得．

试题解析：（1）证明：如图，连接OE，∵OB=OE，∴∠OBE=∠OEB，∵BE平分∠ABC，∴∠OBE=∠EBD，∴∠OEB=∠EBD，∴OE∥BD，∵AB=AC，AD平分∠BAC，∴AD⊥BC，∴∠OEA=∠BDA=90°，∴AD是⊙O的切线；

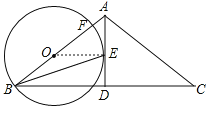
（2）解：∵AB=AC=4，∴OB=OE=OF=2，由（1）可知OE∥BC，且AB=AC，∴∠AOE=∠ABC=∠C=30°，∴==．