题目内容
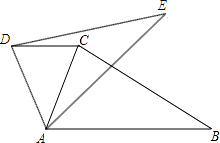
【题目】如图是由射线AB,BC,CD,DE,EA组成的平面图形,则∠1+∠2+∠3+∠4+∠5= . 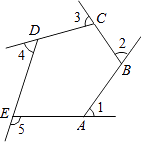
【答案】360°
【解析】解:∠1+∠2+∠3+∠4+∠5 =(180°﹣∠BAE)+(180°﹣∠ABC)+(180°﹣∠BCD)+(180°﹣∠CDE)+(180°﹣∠DEA)
=180°×5﹣(∠BAE+∠ABC+∠BCD+∠CDE+∠DEA)
=900°﹣(5﹣2)×180°
=900°﹣540°
=360°.
故答案为:360°.
首先根据图示,可得∠1=180°﹣∠BAE,∠2=180°﹣∠ABC,∠3=180°﹣∠BCD,∠4=180°﹣∠CDE,∠5=180°﹣∠DEA,然后根据三角形的内角和定理,求出五边形ABCDE的内角和是多少,再用180°×5减去五边形ABCDE的内角和,求出∠1+∠2+∠3+∠4+∠5等于多少即可.

练习册系列答案
相关题目