��Ŀ����
����Ŀ���ڵ�����ABC�У�
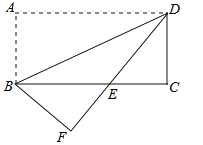
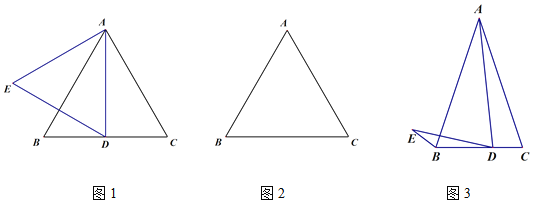
��1����ͼ1������ABCΪ�ȱ������Σ�DΪ�߶�BC�е㣬�߶�AD����ֱ��AB�ĶԳ��߶�Ϊ�߶�AE������DE�����BDE�Ķ���Ϊ___________��
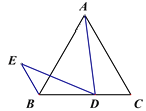
��2������ABCΪ�ȱ������Σ���DΪ�߶�BC��һ���㣨����B��C�غϣ�������AD�����߶�AD�Ƶ�D��ʱ����ת60���õ��߶�DE������BE.
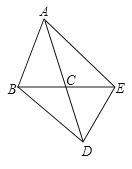
�ٸ���������ͼ2�в�ȫͼ�Σ�
��С��ͨ���۲졢��֤������²⣺�ڵ�D�˶��Ĺ����У�����CD=BE.������ͬѧ�ǵij�����ۣ��γ��˼���֤����˼·��
˼·1��Ҫ֤��CD=BE��ֻ��Ҫ����AE����֤����ADC�ա�AEB��
˼·2��Ҫ֤��CD=BE��ֻ��Ҫ����D��DF��AB����AC��F��֤����ADF�ա�DEB��
˼·3��Ҫ֤��CD=BE��ֻ��Ҫ�ӳ�CB����G��ʹ��BG=CD��֤����ADC�ա�DEG��
����
��ο�����˼·������С��֤��CD=BE.��ֻ��Ҫ��һ�ַ���֤�����ɣ�
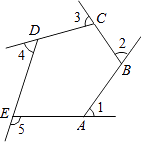
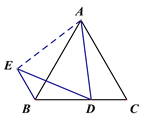
��3��С��ķ���������С������ͼ3����AB=AC=kBC��AD=kDE���ҡ�ADE=��C����ʱС������BE��BD��AC����֮������һ���ĵ�������ϵ�����������ϵ��______________________.��ֱ�Ӹ�����������֤����
���𰸡���1��30�㣻��2���𰸼���������3��k(BE+BD)=AC
�������������������1����AD�ǵȱ�������ABC��BC���ϵ����ߵ�AD��BC����AE��AD����AB�Գƣ��Ӷ�AB��ֱƽ��DE���ɵ���ADE��60�㣬������BDE=30����
��2���ٸ������⻭ͼ���ɣ�
����˼·1��֤����EAB�ա�DAC���ɵó�����.
��3��k(BE+BD)=AC.
�����������1���ߦ�ABC�ǵȱ������Σ�D��BC�ߵ��е�
���BAD=30��
���߶�AD��AE����ֱ��AB�Գ�
��DE��AB
���ADE=60��
����BDE=90��-60��=30����
��2����ͼ���£�
����ͼ������AE.
![]()
![]()
![]()
![]()
![]()
![]()
��3��k(BE+BD)=AC.