题目内容
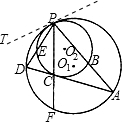
如图，⊙Ol和⊙O2内切于点P，过点P的直线交⊙Ol于点D，交⊙O2于点E，DA与⊙O2相切，切点为C．
（1）求证：PC平分∠APD；
（2）求证：PD•PA=PC2+AC•DC；
（3）若PE=3，PA=6，求PC的长．
（1）求证：PC平分∠APD；
（2）求证：PD•PA=PC2+AC•DC；
（3）若PE=3，PA=6，求PC的长．
（1）过P作两圆的公切线PT，
根据弦切角定理得：∠PCD=∠PBC
∠PCB=∠PDC
∴∠DPC=∠APC，
∴PC平分∠APD；
（2）∵AC•DC=PC•CF，
∴PC2+AC•DC=PC2+PC•CF=PC（PC+CF）=PC•PF．
∵△PDC∽△PFA，
∴PC•PF=PD•PA，
∴PD•PA=PC2+AC•DC；
（3）∵△PCA∽△PEC，
∴
=
，
即PC2=PA•PE，
∵PE=3，PA=6，
∴PC=3
．
根据弦切角定理得：∠PCD=∠PBC
∠PCB=∠PDC
∴∠DPC=∠APC，
∴PC平分∠APD；
（2）∵AC•DC=PC•CF，
∴PC2+AC•DC=PC2+PC•CF=PC（PC+CF）=PC•PF．
∵△PDC∽△PFA，
∴PC•PF=PD•PA，
∴PD•PA=PC2+AC•DC；
（3）∵△PCA∽△PEC，
∴
| PC |
| PE |
| PA |
| PC |
即PC2=PA•PE，
∵PE=3，PA=6，
∴PC=3
| 2 |
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
交点）．设与AB、l、x轴相切的⊙O1的半径为r1，与AC、l、x轴相切的⊙O2半径为r2
