题目内容
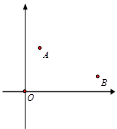
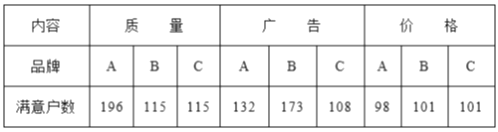
【题目】如图1，在平面直角坐标系xOy中，A，B两点的坐标分别为A（x1，y1），B（x2，y2），由勾股定理得AB2=|x2﹣x1|2+|y2﹣y1|2，所以A，B两点间的距离为：AB=
我们知道，圆可以看成到圆心距离等于半径的点的集合，如图2，在平面直角坐标系xoy中，A（x，y）为圆上任意一点，则A到原点的距离的平方为OA2=|x﹣0|2+|y﹣0|2，当⊙O的半径为r时，⊙O的方程可写为：x2+y2=r2．
问题拓展：如果圆心坐标为P（a，b），半径为r，那么⊙P的方程可以写为 ．
综合应用：
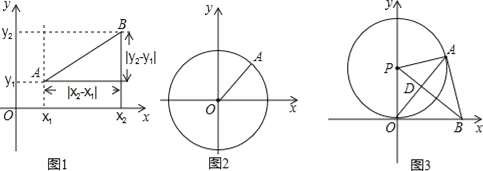
如图3，⊙P与x轴相切于原点O，P点坐标为（0，6），A是⊙P上一点，连接OA，使∠POA=30°，作PD⊥OA，垂足为D，延长PD交x轴于点B，连接AB．
①证明：AB是⊙P的切线；
②是否存在到四点O，P，A，B距离都相等的点Q？若存在，求Q点坐标，并写出以Q为圆心，以OQ为半径的⊙Q的方程；若不存在，说明理由．
【答案】（x﹣a）2+（y﹣b）2=r2；①证明见解析；②存在，Q（3
，3），（x﹣3
）2+（y﹣3）2=36．
【解析】试题分析：问题拓展：直接根据圆的定义即可得出结论；
综合应用：①先判断出△POB≌△PAB，即可得出结论；
②先得出点Q是BP中点，再根据含30°角的直角三角形的性质确定出点B的坐标，进而得出点Q的坐标，
解：问题拓展：根据圆的定义得，（x﹣a）2+（y﹣b）2=r2，
故答案为：（x﹣a）2+（y﹣b）2=r2，
综合应用：①∵PO=PA PD⊥OA，
∴∠OPD=∠APD，
在△POB和△PAB中
，
∴△POB≌△PAB，
∴∠PAB=∠POB=90°，
∴PA⊥AB
∴AB是⊙P的切线，
②存在到四点O，P，A，B距离都相等的点Q，
当点Q在线段BP中点时
∵∠POB=∠PAB=90°，
∴QO=QP=QA=QB
∴此时点Q到四点O，P，A，B距离都相等
∵PB⊥OA，∠POB=90°，∠POA=30°
∴∠PBO=30°．
∴在Rt△POB中，OP=6，
∴OB=
OP=6
，PB=2PO=12
∴B点坐标为（6
，0），
∵Q是PB中点，P（0，6），B（6
，0），
∴Q点坐标为（3
，3）
∴OQ=
PB=6
∴以Q为圆心，OQ为半径的⊙Q的方程为（x﹣3
）2+（y﹣3）2=36．
