题目内容
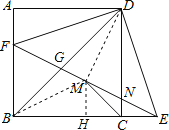
【题目】如图,正方形ABCD中,F为AB上一点,E是BC延长线上一点,且AF=EC,连接EF,DE,DF,M是FE中点,连结MC,设FE与DC相交于点N.则4个结论:①DN=DG;②△BFG∽△EDG∽△BDE;③CM垂直BD;④若MC=![]() ,则BF=2;正确的结论有( )个
,则BF=2;正确的结论有( )个
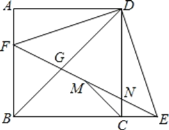
A.4B.3C.2D.1
【答案】B
【解析】
根据正方形的性质可得AD=CD,然后利用“边角边”证明△ADF和△CDE全等,根据全等三角形对应角相等可得∠ADF=∠CDE,然后求出∠EDF=∠ADC=90°,而∠DGN=45°+∠FDG,∠DNG=45°+∠CDE,∠FDG不一定等于∠CDE,于是∠DGN不一定等于∠DNG,判断出①错误;
根据全等三角形对应边相等可得DE=DF,然后判断出△DEF是等腰直角三角形,根据等腰直角三角形的性质可得∠DEF=45°,再根据两组角对应相等的三角形相似得到△BFG∽△EDG∽△BDE,判断出②正确;
连接BM、DM,根据直角三角形斜边上的中线等于斜边的一半可得![]() 然后判断出直线CM垂直平分BD,判断出③正确;
然后判断出直线CM垂直平分BD,判断出③正确;
过点M作MH⊥BC于H,得到∠MCH=45°,然后求出MH,再根据三角形的中位线平行于第三边并且等于第三边的一半可得BF=2MH,判断出④正确.
在正方形ABCD中,AD=CD,
在△ADF和△CDE中,
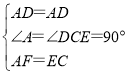 ,
,
∴△ADF≌△CDE(SAS),
∴∠ADF=∠CDE,DE=DF,
∴∠EDF=∠FDC+∠CDE=∠FDC+∠ADF=∠ADC=90°,
∴∠DEF=45°,
∵∠DGN=45°+∠FDG,∠DNG=45°+∠CDE,∠FDG≠∠CDE,
而∠FDG与∠CDE不一定相等,
∴∠DGN与∠DNG不一定相等,故判断出①错误;
∵△DEF是等腰直角三角形,
∵∠ABD=∠DEF=45°,∠BGF=∠EGD(对顶角相等),
∴△BFG∽△EDG,
∵∠DBE=∠DEF=45°,∠BDE=∠EDG,
∴△EDG∽△BDE,
∴△BFG∽△EDG∽△BDE,故②正确;
如图,连接BM、DM
.
∵△AFD≌△CED,
∴∠FDA=∠EDC,DF=DE,
∴∠FDE=∠ADC=90°,
∵M是EF的中点,
∴![]()
∵![]()
∴MD=MB,
在△DCM与△BCM中,
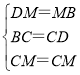 ,
,
∴△DCM≌△BCM(SSS),
∴∠BCM=∠DCM,
∴CM在正方形ABCD的角平分线AC上,
∴MC垂直平分BD;故③正确;
过点M作MH⊥BC于H,则∠MCH=45°,
∵![]() ,
,
∴![]() ,
,
∵M是EF的中点,BF⊥BC,MH⊥BC,
∴MH是△BEF的中位线,
∴BF=2MH=2,故④正确;
综上所述,正确的结论有②③④.
故选:B.

 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案【题目】近年来网约车十分流行,初三某班学生对“美团”和“滴滴”两家网约车公司各10名司机月收入进行了一项抽样调查,司机月收入(单位:千元)如图所示:

根据以上信息,整理分析数据如下:
平均月收/千元 | 中位数/千元 | 众数/千元 | 方差/千元 | |
“美团” | ① | 6 | 6 | 1.2 |
“滴滴” | 6 | ② | 4 | ③ |
(1)完成表格填空:①__________②__________③__________
(2)若从两家公司中选择一家做网约车司机,你会选哪家公司,并说明理由.