题目内容
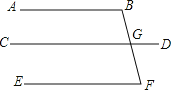
【题目】如图：已知∠B＝∠BGD，∠DGF＝∠F，求证：∠B+∠F＝180°．
请你认真完成下面的填空．
证明：∵∠B＝∠BGD （ 已知 ）
∴AB∥CD （ ）
∵∠DGF＝∠F；（ 已知 ）
∴CD∥EF （ ）
∴AB∥EF （ ）
∴∠B+∠F＝180°（ ）．
【答案】内错角相等，两直线平行；内错角相等，两直线平行；平行于同一条直线的两条直线平行；两直线平行，同旁内角互补.
【解析】
观察图形，由∠B＝∠BGD，根据内错角相等，两直线平行，即可证得AB∥CD，又由∠DGF=∠F，根据内错角相等，两直线平行，可证得CD∥EF，由平行于同一条直线的两条直线平行，则得AB∥EF，再根据两直线平行 同旁内角互补，易得∠B＋∠F＝180°．
证明：∵∠B＝∠BGD（已知），
∴AB∥CD（内错角相等，两直线平行），
∵∠DGF＝∠F（已知），
∴CD∥EF（内错角相等，两直线平行），
∴AB∥EF（平行于同一条直线的两条直线平行）
∴∠B+∠F＝180°（两直线平行，同旁内角互补）；
故答案为：内错角相等，两直线平行；内错角相等，两直线平行；平行于同一条直线的两条直线平行；两直线平行，同旁内角互补．
练习册系列答案
冲刺100分1号卷系列答案
相关题目
