ЬтФПФкШн
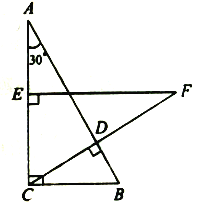
ЁОЬтФПЁПзлКЯЬНОПЃКШчЭМ1ЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌХзЮяЯпy=Љ![]() +bx+8гыxжсНЛгкЕуAЃЈЉ6ЃЌ0ЃЉКЭЕуBЃЈЕуAдкЕуBзѓВрЃЉЃЌгыyжсНЛгкЕуCЃЌЕуPЮЊЯпЖЮAOЩЯЕФвЛИіЖЏЕуЃЌЙ§ЕуPзїxжсЕФДЙЯпlгыХзЮяЯпНЛгкЕуEЃЌСЌНгAEЁЂECЃЎ
+bx+8гыxжсНЛгкЕуAЃЈЉ6ЃЌ0ЃЉКЭЕуBЃЈЕуAдкЕуBзѓВрЃЉЃЌгыyжсНЛгкЕуCЃЌЕуPЮЊЯпЖЮAOЩЯЕФвЛИіЖЏЕуЃЌЙ§ЕуPзїxжсЕФДЙЯпlгыХзЮяЯпНЛгкЕуEЃЌСЌНгAEЁЂECЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФБэДяЪНМАЕуCЕФзјБъЃЛ
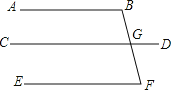
ЃЈ2ЃЉСЌНгACНЛжБЯпlгкЕуDЃЌдђдкЕуPдЫЖЏЙ§ГЬжаЃЌЕБЕуDЮЊEPжаЕуЪБЃЌSЁїADPЃКSЁїCDE=ЁЁ ЁЁЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌЕБECЁЮxжсЪБЃЌЕуPЭЃжЙдЫЖЏЃЌДЫЪБЃЌдкХзЮяЯпЩЯЪЧЗёДцдкЕуGЃЌЪЙЕУвдЕуAЁЂEЁЂGЮЊЖЅЕуЕФШ§НЧаЮЪЧжБНЧШ§НЧаЮЃПШєДцдкЃЌЧыЧѓГіЕуGЕФзјБъЃЌШєВЛДцдкЃЌЫЕУїРэгЩЃЎ

ЁОД№АИЁПЃЈ1ЃЉCЃЈ0ЃЌ8ЃЉЃЈ2ЃЉ1ЃК2ЃЈ3ЃЉДцдкЕуGЪЙЕУвдЕуAЃЌEЃЌGЮЊЖЅЕуЕФШ§НЧаЮЮЊжБНЧШ§НЧаЮЃЌЗћКЯЬѕМўЕФGЕуЕФзјБъЮЊGЃЈ![]() ЃЌ
ЃЌ ![]() ЃЉЛђGЃЈ
ЃЉЛђGЃЈ![]() ЃЌЉ
ЃЌЉ![]() ЃЉЃЌ
ЃЉЃЌ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉгУД§ЖЈЯЕЪ§ЗЈЧѓГіХзЮяЯпНтЮіЪНЃЌСю![]() ЧѓГі
ЧѓГі![]() жсНЛЕузјБъЃЛ
жсНЛЕузјБъЃЛ
ЃЈ2ЃЉЯШШЗЖЈГіжБЯп![]() НтЮіЪНЮЊ
НтЮіЪНЮЊ![]() ЩшГіЕуEЕФзјБъЃЌБэЪОГіЕу
ЩшГіЕуEЕФзјБъЃЌБэЪОГіЕу![]() ЖјЕуDдкжБЯпACЩЯЃЌСаГіЗНГЬ
ЖјЕуDдкжБЯпACЩЯЃЌСаГіЗНГЬ![]()
ЧѓГі![]() ЃЌДгЖјЕУГіНсТлЃЛ
ЃЌДгЖјЕУГіНсТлЃЛ
ЃЈ3ЃЉЯШЧѓГіЕу![]() ЕФзјБъЃЌдйЗжСНжжЧщПіМЦЫуЂёЁЂЕБ
ЕФзјБъЃЌдйЗжСНжжЧщПіМЦЫуЂёЁЂЕБ![]() ЪБЃЌХаЖЯГіЁїEMGЁзЁїAPEЃЌЕУГіБШР§ЪНЧѓНтМДПЩЃЌЂђЁЂЕБ
ЪБЃЌХаЖЯГіЁїEMGЁзЁїAPEЃЌЕУГіБШР§ЪНЧѓНтМДПЩЃЌЂђЁЂЕБ![]() ЪБЃЌХаЖЯГіЁїGNAЁзЁїAPEЃЌЕУЕНБШР§ЪНМЦЫуЃЎ
ЪБЃЌХаЖЯГіЁїGNAЁзЁїAPEЃЌЕУЕНБШР§ЪНМЦЫуЃЎ
ЪдЬтНтЮіЃК(1)ЁпЕуA(6,0)дкХзЮяЯп![]() ЩЯЃЌ
ЩЯЃЌ
Ёр![]()
![]()
Ёр![]()
Сюx=0ЃЌy=8ЃЌ
ЁрC(0,8)
(2)Щш![]()
ЁрP(m,0)ЃЌ
ЁпЕуDЮЊEPжаЕуЃЌ
ЁрDP=DE, ![]()
ЁпA(6,0),C(0,8)ЃЌ
ЁржБЯпACНтЮіЪНЮЊ![]()
ЁпЕуDдкжБЯпACЩЯЃЌ
Ёр![]()
Ёрm=6(
ЁрP(4,0)
ЁрAP=2ЃЌOP=4ЃЌ
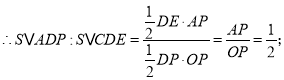
ЙЪД№АИЮЊ1:2
(3)ДцдкЕуGЪЙЕУвдЕуAЃЌEЃЌGЮЊЖЅЕуЕФШ§НЧаЮЮЊжБНЧШ§НЧаЮЃЌ
СЌНгEGЃЌAGЃЌзїGMЁЭlЃЌGNЁЭxжсЃЌ
ЁпECЁЮxжсЃЌ
ЁрEP=CO=8ЃЌ
Абy=8ДњШы![]()
Ёр![]()
Ёрx=0(Щс)ЃЌЛђx=2ЃЌ
ЁрP(2,0)ЃЌ
ЁрAP=AOPO=4ЃЌ
ЂёЁЂШчЭМ1ЃЌ
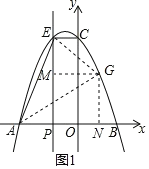
ЕБ![]() ЪБЃЌ
ЪБЃЌ
Ёр![]()
Ёп![]()
ЁрЁЯMEG=ЁЯEAPЃЌ
Ёп![]()
ЁрЁїEMGЁзЁїAPEЃЌ
Ёр![]()
ЩшЕу![]()
![]()
Ёр![]()
MG=PN=PO+ON=2+mЃЌ
![]()
Ёр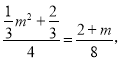 Ёрm=2(Щс)Лђ
Ёрm=2(Щс)Лђ![]()
Ёр![]()
ЂђЁЂШчЭМ2ЃЌ
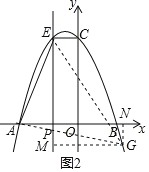
ЕБ![]() ЪБЃЌ
ЪБЃЌ
Ёр![]()
Ёп![]()
ЁрЁЯNAG=ЁЯAEPЃЌ
Ёп![]()
ЁрЁїGNAЁзЁїAPEЃЌ
Ёр![]()
ЩшЕу![]()
![]()
ЁрAN=AO+ON=6+nЃЌ
Ёп![]()

Ёрn=6(Щс),Лђ![]()
Ёр![]()
ЗћКЯЬѕМўЕФGЕуЕФзјБъЮЊ![]() Лђ
Лђ![]()

ЁОЬтФПЁПЯТБэИјГіСЫ1Ар6УћбЇЩњЕФЩэИпЧщПігыШЋАрЦНОљЩэИпЕФВюжЕЃЈЕЅЮЛЃКРхУзЃЉ
бЇЩњ | A | B | C | D | E | F |
ЩэИп | 157 | 162 | 159 | 152 | 163 | 164 |
ЩэИпгыШЋАрЦНОљЩэИпЕФВюжЕ | -3 | +2 | -1 | a | +3 | b |
ЃЈ1ЃЉСаЪНМЦЫуБэжаЪ§ОнaКЭb
ЃЈ2ЃЉет6УћбЇЩњЕФЦНОљЩэИпгыШЋАрбЇЩњЕФЦНОљЩэИпЯрБШЃЌдкЪ§жЕЩЯгаЪВУДЙиЯЕЃПЃЈЭЈЙ§МЦЫуЛиД№ЃЉ