Question

【题目】如图，D为△ABC内一点，CD平分∠ACB，BD⊥CD，∠A＝∠ABD，若AC＝5，BC＝3，则CD的长是_______.

Answer 1

【答案】

【解析】

延长BD，与AC交于点E，利用ASA得到三角形BCD与三角形ECD全等，利用全等三角形对应边相等得到CE=CB，BD=ED，再由已知角相等，利用等角对等边得到AE=BE，由AC-CE求出AE的长，进而求出BD的长，利用勾股定理求出CD即可．

解：延长BD，与AC交于点E，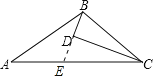

∵CD平分∠ACB，
∴∠ACD=∠BCD，
∵BD⊥CD，
∴∠BDC=∠EDC=90°，
在△BCD和△ECD中，

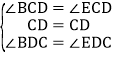
∴△BCD≌△ECD（ASA），
∴BC=EC=3，BD=DE，
∵∠A=∠ABE，
∴AE=BE=AC-EC=AC-BC=5-3=2，
∴BD=1，
在Rt△BDC中，BD=1，BC=3，
根据勾股定理得：CD=．
故答案为： ．