题目内容
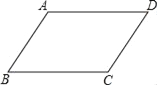
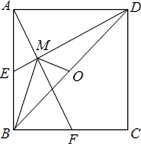
【题目】如图,在菱形ABCD中,点E,F,G,H分别是边AB,BC,CD和DA的中点,连接EF,FG,GH和HE,若EH=2EF=2,则菱形ABCD的边长为( )
A. ![]() B. 2
B. 2 ![]() C. 2 D. 4
C. 2 D. 4
【答案】A
【解析】
连接AC、BD交于O,根据菱形的性质得到AC⊥BD,OA=OC,OB=OD,根据三角形中位线定理、矩形的判定定理得到四边形EFGH是矩形,根据勾股定理计算即可.
连接AC、BD交于O,
∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC,OB=OD,
∵点E、F、G、H分别是边AB、BC、CD和DA的中点,
∴EF=![]() AC,EH=
AC,EH=![]() BD, EF∥AC,EH∥BD,
BD, EF∥AC,EH∥BD,
∴四边形EFGH是平行四边形,EH⊥EF,
∴四边形EFGH是矩形,
∵EH=2EF=2,
∴OB=2OA=2,
∴AB=![]() .
.
故选:A.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
【题目】近期,我市持续出现雾霾天气,给广大市民的工作和生活造成了严重的影响.为此,“雾霾天气的主要成因”就成为了某校环保小组调查研究的课题,他们随机调查了部分市民,并对调查结果进行了整理,绘制了如图所示的不完整的统计图表.请根据图表中提供的信息解答下列问题:
级别 | 观点 | 频数(人数) |
A | 大气气压低,空气不流动 |
|
B | 地面灰尘大,空气湿度低 |
|
C | 汽车尾部排放 |
|
D | 工厂造成污染 |
|
E | 其他 |
|
调查结果扇形统计图
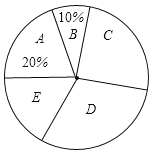
(1)填空:![]() ______,
______,![]() ______;
______;
(2)求出扇形统计图中E组所占的百分比以及扇形统计图中区域D所对应的扇形圆心角度数;