题目内容
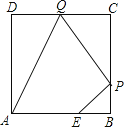
【题目】已知,如图,正方形![]() 的边长为4厘米,点
的边长为4厘米,点![]() 从点
从点![]() 出发,经
出发,经![]() 沿正方形的边以2厘米/秒的速度运动;同时,点
沿正方形的边以2厘米/秒的速度运动;同时,点![]() 从点
从点![]() 出发以1厘米/秒的速度沿
出发以1厘米/秒的速度沿![]() 向点
向点![]() 运动,设运动时间为t秒,
运动,设运动时间为t秒,![]() 的面积为
的面积为![]() 平方厘米.
平方厘米.
(1)当![]() 时,
时,![]() 的面积为__________平方厘米;
的面积为__________平方厘米;
(2)求![]() 的长(用含
的长(用含![]() 的代数式表示);
的代数式表示);
(3)当点![]() 在线段
在线段![]() 上运动,且
上运动,且![]() 为等腰三角形时,求此时
为等腰三角形时,求此时![]() 的值;
的值;
(4)求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
【答案】(1)8;(2)BP=![]() ;(3)
;(3)![]() ;(4)S
;(4)S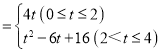 .
.
【解析】
(1)先确定当t=2时P和Q的位置,再利用三角形面积公式可得结论;
(2)分两种情况表示BP的长;
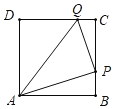
(3)如图2,根据CQ=CP列方程可解答;
(4)分两种情况:
①当0≤t≤2时,P在AB上,如图3,②当2<t≤4时,P在BC上,如图4,根据三角形面积公式可得结论.
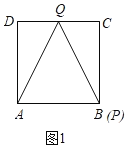
(1)当t=2时,点P与B重合,Q在CD上,如图1,∴△APQ的面积![]() 8(平方厘米).
8(平方厘米).
故答案为:8;
(2)分两种情况:
当0≤t≤2时,P在AB上,BP=AB﹣AP=4﹣2t,当2<t≤4时,P在BC上,BP=2t﹣4;
综上所述:BP=![]() ;
;
(3)如图2.
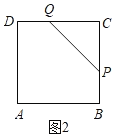
∵△PCQ为等腰三角形,∴CQ=CP,即t=8﹣2t,t![]() ,∴当点P在线段BC上运动,且△PCQ为等腰三角形时,此时t的值是
,∴当点P在线段BC上运动,且△PCQ为等腰三角形时,此时t的值是![]() 秒;
秒;
(4)分两种情况:
①当0≤t≤2时,P在AB上,如图3.
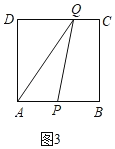
S![]() 4t
4t
②当2<t≤4时,P在BC上,如图4.
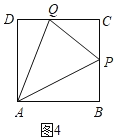
S=S正方形ABCD﹣S△ABP﹣S△CPQ﹣S△ADQ=4×4![]() t2﹣6t+16;
t2﹣6t+16;
综上所述:S与t之间的函数关系式为:S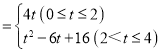 .
.

 名校课堂系列答案
名校课堂系列答案【题目】北国超市销售每台进价分别为400元、350元的![]() 两种型号的豆浆机.下表是近两周的销售情况:
两种型号的豆浆机.下表是近两周的销售情况:
销售数量:
销售时段 | 销售数量 | 销售收入 | |
|
| ||
第一周 | 3台 | 5台 | 3500元 |
第二周 | 4台 | 10台 | 6000元 |
(进价、售价均保持不变,利润=销售收入-进价)
(1)求![]() 两种型号的豆浆机的销售单价;
两种型号的豆浆机的销售单价;
(2 )若第三周该超市采购这两种型号的豆浆机共20台, 并且B型号的台数比A型号的台数的2倍少1 ,如果这20台豆浆机全部售出,求这周销售的利润;
(3)若恰好用8000元采购这两种型号的豆浆机,问有哪几种进货方案? ( 要求两种型号都要采购)