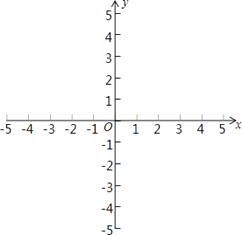题目内容
【题目】在等腰![]() 中,
中,![]() ,
,![]() ,点
,点![]() ,点
,点![]() 分别是
分别是![]() 轴,
轴,![]() 轴上两个动点,直角边
轴上两个动点,直角边![]() 交
交![]() 轴于点
轴于点![]() ,斜边
,斜边![]() 交
交![]() 轴于点
轴于点![]() .
.
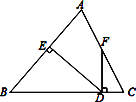
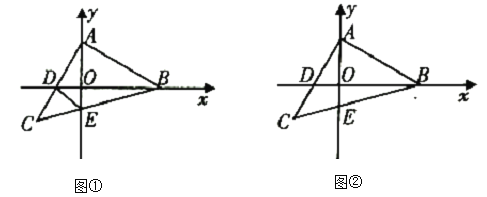
(1)如图①,当等腰![]() 运动到使点
运动到使点![]() 恰为
恰为![]() 中点时,连接
中点时,连接![]() ,求证:
,求证:![]() ;
;
(2)如图②,当等腰![]() 运动到使
运动到使![]() 时,
时,![]() 点的横坐标为
点的横坐标为![]() ,
,![]() .在
.在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 为等腰三角形?若存在,请直接写出点
为等腰三角形?若存在,请直接写出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
【答案】(1)证明见解析;(2)存在,P点的坐标为![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
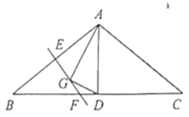
(1)过点C作CG⊥AC交y轴于点G,则△ACG≌△ABD(ASA),即得CG=AD=CD,∠ADB=∠AGC,由∠DCE=∠GCE=45°,可证△DCE≌△GCE(SAS)得∠CDE=∠AGC,从而得到结论;
(2)根据含30°的直角三角形的特点解直角三角形,分别求出OA和AB,然后设P(a,0)分情况讨论即可.
解:(1)证明:如图,过点C作CG⊥AC交y轴于点G,
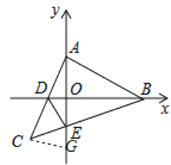
∵D为AC的中点,
∴AD=CD,
∵AC=AB,![]() ,
,
∴∠ACB=∠ABC=45°,
∵CG⊥AC ,
∴∠ACG=90°,∠CAG+∠AGC=90°,
∵∠AOD=90°,
∴∠ADO+∠DAO=90°,
∴∠AGC=∠ADO,
在△ACG和△ABD中,
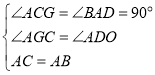
∴△ACG≌△ABD(AAS),
∴CG=AD=CD,∠ADB=∠AGC,
∵∠ACB=45°,∠ACG=90°,
∴∠DCE=∠GCE=45°,
在△DCE和△GCE中,
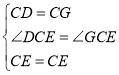
∴△DCE≌△GCE(SAS),
∴∠CDE=∠AGC,
∴∠ADB=∠CDE;
(2)存在,
∵![]() ,
,![]() ,
,
∴![]() ,即
,即![]() ,
,
∴在Rt△AOB中根据勾股定理![]() ,
,
即![]() ,
,
解得OA=3,AB=2OA=6,
∴![]() ,
,
设P(a,0),则![]() ,
,
①若AP=BP,则AP2=BP2,即
![]() ,解得
,解得![]()
∴![]() ,
,
②若AP=AB,则AP2=AB2,即
![]() ,解得
,解得![]() 或
或![]() (舍去),
(舍去),
∴![]() ,
,
③若AB=AB,则AB2=AB2,即
![]() ,
,
解得![]() 或
或![]() ,
,
∴![]() 或
或![]() ,
,
综上所述P点的坐标为![]() 或
或![]() 或
或![]() 或
或![]() .
.