题目内容
【题目】如图，在
中，
，
，点
在边
上，
，点
为
的中点，点
为边
上的动点，则使四边形
周长最小的点的坐标为（ ）
A.
B.
C.
D.
【答案】C
【解析】
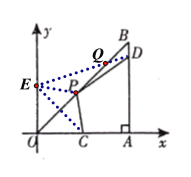
如图（见解析），在y轴上取点E，使得
，连接CE、EP、ED，ED交OB于点Q，先根据等腰三角形的三线合一性质得出OB是CE的垂直平分线，再根据两点之间线段最短得当点P与点Q重合时，四边形PCAD周长最小，最后求直线ED与直线OB的交点即可.
如图，在y轴上取一点E，使得，连接CE、EP、ED，ED交OB于点Q
则点E的坐标为
点D的坐标为
，
是等腰直角三角形
OB是
的角平分线
点
为
的中点
，即点C的坐标为
是CE的垂直平分线（等腰三角形的三线合一性质）
四边形PCAD周长：
由两点之间线段最短得：当P与点Q重合时，
最小，最小值为
，此时四边形PCAD的周长最小
设直线OB的解析式为
将
代入得
，解得
则直线OB的解析式为
设直线ED的解析式为
将
代入得
，解得
则直线ED的解析式为
联立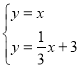
，解得
则点Q的坐标为
故选：C.
练习册系列答案
快捷英语周周练系列答案
相关题目
