Question

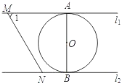
【题目】如下图，已知直线分别与轴，轴交于，两点，直线：交于点.

（1）求，两点的坐标；

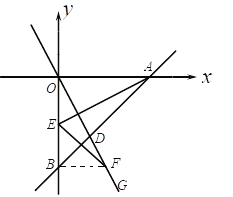
（2）如图1，点E是线段OB的中点，连结AE，点F是射线OG上一点， 当，且时，求的长；

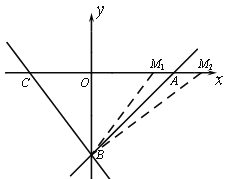
（3）如图2，若，过点作∥，交轴于点，此时在轴上是否存在点，使，若存在，求出点的坐标；若不存在，请说明理由.

Answer 1

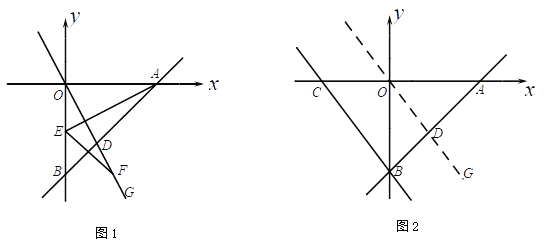
【答案】（1）A（4，0），B（0，-4）（2）EF=（3）

【解析】

（1）根据直线与坐标轴的坐标特点即可求解；

（2）连结BF，根据题意可证明△AOE≌△OBF，得到BF=OE，求出BF=2，再利用在Rt△BEF中，由勾股定理求得EF=；

（3）根据平行求出直线BC的函数表达式为 得到C(-3,0)，OC=3再分当M1在A点左侧，当M点在A点右侧分别进行求解.

(1) 直线与轴，轴分别相交于A，B两点，

时， ；时，

A（4，0），B（0，-4）.

（2）连结BF，由(1) ，得OA=OB，∠AOB=,

∠BOF+∠AOF=,

OF⊥AE，

∠AOF+∠EAO=.

∠BOF=∠EAO，

又AE=OF，OA=OB，

△AOE≌△OBF.

∠OBF=∠AOE=，BF=OE.

E是OB的中点 ,

OE=OB=2.

BF=2.

在Rt△BEF中，由勾股定理，EF2=BF2+BE2=22+22=8.

又EF>0,

EF=.

(3)∵BC∥OG，

∴直线BC的函数表达式为

又B(0，-4),

∴.

∴

令

得.

即C(-3,0).

∴OC=3.

故①当M1在A点左侧，在OA上取OM1=3，则M1，C关于y轴对称.

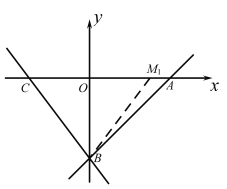
∴∠MBO=∠CBO.

∵OA=OB，∠AOB=90°,

∴∠ABO=45°.

而∠M1BO+∠ABM1=∠ABO=45°,

即∠CBO+∠ABM1=45°.

∴M1即为所求的点.

∴

②当M点在A点右侧，满足∠CBO+∠ABM2=45°时，又∠ABO=45°,

∴∠CBM2=∠CBO+∠ABM2+∠ABO=45°+45°=90°.

设M2(m，0),

在Rt△CBM2与Rt△BOM2中，由勾股定理，得：

即

∴

∴

∴