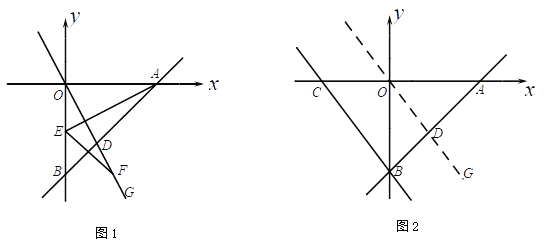��Ŀ����
����Ŀ������ֱ����ABC����MAD�У���BAC=��DMA=90�㣬����BM��CD����B��M��D���㹲��

��1������D����M��BC���·���CD��BDʱ����ͼ������֤��BM+CD=AM������ʾ���ӳ�DB����N��ʹMN=MD������AN����
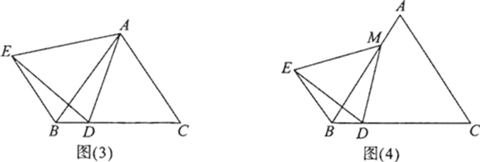
��2������D��AC���Ҳ࣬��M����ABC�ڲ�ʱ����ͼ��������D��AB����࣬��M����ABC�ⲿʱ����ͼ������ֱ��д���߶�BM��CD��AM֮���������ϵ������Ҫ֤����
��3���ڣ�1������2�������£���E��AB�е㣬MF����AMD�Ľ�ƽ���ߣ�����EF����EF=2MF=6����CD=�� ����
���𰸡���1��֤����������2������D��AC���Ҳ࣬��M����ABC�ڲ�ʱ��BM=CD+AM��3��12-6![]()
��������
��1���ӳ�DB����N��ʹMN=MD���������֤��AND�ǵ���ֱ�������Σ��ɵá�NAD=��BAC=90�㣬AN=AD������֤��ABN�ա�ACD���ɵ�BN=CD������ۿɵã�
��2������D��AC���Ҳ࣬��M�ڡ�ABC�ڲ�ʱ�������߶�BM�Ͻ�ȡMN=DM���������֤��AND�ǵ���ֱ�������Σ��ɵá�NAD=��BAC=90�㣬AN=AD������֤��ABN�ա�ACD���ɵ�BN=CD�����ɵ�BM=CD+AM������D��AB����࣬��M�ڡ�ABC�ⲿʱ���ӳ�DM��N��ʹMN=DM���������֤��AND�ǵ���ֱ�������Σ��ɵá�NAD=��BAC=90�㣬AN=AD������֤��ABN�ա�ACD���ɵ�BN=CD�����ɵ�CD=BM+AM
��3��������ɵ�EF����λ�ߣ��������ۣ������ϵʽ����CD�ij��ȣ�
��1���ӳ�DB����N��ʹMN=MD������AN,
������ֱ����ABC����MAD,
��AM=MD��AB=AC����ADM=45��=��MAD,
��MN=MD����DMA=90�㣬AM=AM,
���AMN�ա�AMD,
��AD=AN����NAM=��MAD=45��,
���NAD=90��,
�ߡ�NAD=��BAC=90��,
���NAB=��CAD����AN=AD��AB=AC,
���ABN�ա�ACD,
��BN=CD,
��MN=BM+BN,
��AM=MD=BM+CD,
��2������D��AC���Ҳ࣬��M����ABC�ڲ�ʱ��BM=CD+AM,
��ͼ�����߶�BM�Ͻ�ȡMN=DM,
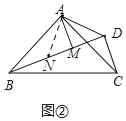
������ֱ����ABC����MAD,
��AM=MD��AB=AC����ADM=45��=��MAD,
��MN=DM,
��AM=DM=MN������AMD=90��,
���AND=��ADN=��NAM=��DAM=45��,
��AN=AD����NAD=90��,
�ߡ�NAD=��BAC=90��,
���BAN=��DAC����AN=AD��AB=AC,
���ABN�ա�ACD,
��BN=CD,
��BM=BN+MN,
��BM=CD+AM,
����D��AB����࣬��M����ABC�ⲿʱ��CD=BM+AM,
��ͼ���ӳ�DM��N��ʹMN=DM��
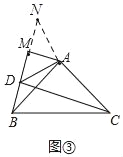
������ֱ����ABC����MAD,
��AM=MD��AB=AC����ADM=45��=��MAD,
��MN=DM,
��AM=DM=MN������AMD=90��,
���AND=��ADN=��NAM=��DAM=45��,
��AN=AD����NAD=90��,
�ߡ�NAD=��BAC=90��,
���BAN=��DAC����AN=AD��AB=AC,
���ABN�ա�ACD,
��BN=CD,
��BN=BM+MN,
��CD=BM+AM,
��3����MF����AMD�Ľ�ƽ���ߣ���DMA=90�㣬AM=DM,
��AF=DF=MF�ҵ�E��AB�е�,
��BD=2EF=12��
��EF=2MF=6,
��MF=3,
��AF=DF=MF=3,
��AM=DM=3![]() ,
,
����D����M��BC���·���CD��BDʱ��AM=BM+CD,
��CD=3![]() ����12��3
����12��3![]() ��=6
��=6![]() ��12��0,
��12��0,
�ʲ����������ĵ�D,
����D��AB����࣬��M����ABC�ⲿʱ��BM=CD+AM,
��CD=BM��AM=12��6![]() ,
,
����D��AB����࣬��M����ABC�ⲿʱ��CD=BM+AM,
��AB��DM,
�������������ĵ�D,
����������CD=12��6![]() ,
,
�ʴ�Ϊ12��6![]() .
.

 53���ò�ϵ�д�
53���ò�ϵ�д�����Ŀ���������������������ij����2000��������ײ��̳�����Ϊ�˹�������ܲ������������ﲶ�����������õ����±������ݣ�
������� | ƽ��ÿ��������� | |
��һ�β��� | 10 | 1.7ǧ�� |
�ڶ��β��� | 25 | 1.8ǧ�� |
�����β��� | 15 | 2.0ǧ�� |
����������������ijɻ�����95%����
(1)������������ƽ��ÿ����Լ����ǧ�ˣ�
(2)��������������ܲ����Ƕ���ǧ�ˣ�
����Ŀ��Сӱ��С����λͬѧ��ѧϰ��������ʱ����Ͷ�����ӣ��ʵؾ��ȵ������壩ʵ�飬���ǹ�����![]() ��ʵ�飬ʵ��Ľ�����£�
��ʵ�飬ʵ��Ľ�����£�
���ϵĵ��� |
|
|
|
|
|
|
���ֵĴ��� |
|
|
|
|
|
|
![]() ������
������![]() �㳯������Ƶ�ʺ���
�㳯������Ƶ�ʺ���![]() �㳯������Ƶ�ʣ�
�㳯������Ƶ�ʣ�
![]() Сӱ˵��������ʵ�飬һ��ʵ���г���
Сӱ˵��������ʵ�飬һ��ʵ���г���![]() �㳯�ϵĸ����������С��˵�������Ͷ��
�㳯�ϵĸ����������С��˵�������Ͷ��![]() �Σ���ô����
�Σ���ô����![]() �㳯�ϵĴ���������
�㳯�ϵĴ���������![]() �Σ���Сӱ��С���˵����ȷ��Ϊʲô��
�Σ���Сӱ��С���˵����ȷ��Ϊʲô��
![]() Сӱ��С���Ͷ��һö���ӣ����б�����״ͼ�ķ��������ö���ӳ��ϵĵ���֮��Ϊ
Сӱ��С���Ͷ��һö���ӣ����б�����״ͼ�ķ��������ö���ӳ��ϵĵ���֮��Ϊ![]() �ı����ĸ��ʣ�
�ı����ĸ��ʣ�
����Ŀ����7�֣�ij��ѧ1000��ѧ���μ���������֪ʶ��������Ϊ���˽Ȿ�ξ����ɼ���������г�ȡ�˲���ѧ���ijɼ����÷�ȡ����������Ϊ100�֣���Ϊ��������ͳ�ƣ�����������ͼƵ���ֲ�����Ƶ���ֲ�ֱ��ͼ���������Ҿֲ�����������������ʾ����������ݣ��������������⣺
�ɼ����� | Ƶ�� | Ƶ�� |
50��x��60 | 8 | 0.16 |
60��x��70 | 12 | a |
70��x��80 | �� | 0.5 |
80��x��90 | 3 | 0.06 |
90��x��100 | b | c |
�ϼ� | �� | 1 |
��1��д��a��b��c��ֵ��
��2���������1000��ѧ�����ж����˵ľ����ɼ�������70�֣�
��3����ѡȡ�������У��Ӿ����ɼ���80�����ϣ���80�֣���ͬѧ�������ȡ����ͬѧ�μӻ���֪ʶ�������������ȡ��2��ͬѧ����ͬһ��ĸ��ʣ�