题目内容
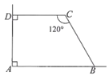
【题目】如图，利用一个直角墙角修建一个梯形储料场ABCD，其中∠C＝120°．若新建墙BC与CD总长为12m，则该梯形储料场ABCD的最大面积是（ ）
A.18m2B.
m2C.
m2D.
m2
【答案】C
【解析】
过点C作CE⊥AB于E，则四边形ADCE为矩形，CD=AE=x，∠DCE=∠CEB=90°，则
∠BCE=∠BCD-∠DCE=30°，BC=12-x，由直角三角形的，性质得出
得出
，又梯形面积公式求出梯形ABCD的面积S与x之间的函数关系式，根据二次函数的性质求解.
解：如图，过点C作CE⊥AB于E，
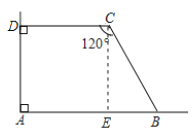
则四边形ADCE为矩形，CD=AE=x，∠DCE=∠CEB=90°，则∠BCE=∠BCD-∠DCE=30°，BC=12-x，
在Rt△CBE中，∵∠CEB=90°，
∴梯形ABCD面积
∴当x=4时，S最大=24
．
即CD长为4 m时，使梯形储料场ABCD的面积最大为24 m2；
故选：C．
练习册系列答案
相关题目
