题目内容
【题目】如图,⊙O是△ABC的外接圆,AB=AC=10,BC=12,P是![]() 上的一个动点,过点P作BC的平行线交AB的延长线于点D.
上的一个动点,过点P作BC的平行线交AB的延长线于点D.
(1)当点P在什么位置时,DP是⊙O的切线?请说明理由;
(2)当DP为⊙O的切线时,求线段DP的长.

【答案】(1)当点P 是![]() 的中点时,DP是⊙O的切线(2)
的中点时,DP是⊙O的切线(2)![]()
【解析】试题分析:(1)根据题意猜想当点P是![]() 的中点时,DP是⊙O的切线,因为DP∥BC,所以只需要证明PA⊥BC,可得DP⊥PA,而在△ABC中利用三线合一可证PA⊥BC;(2)连接OB,设PA交BC于点E.在RtΔABE和RtΔOBE中,由勾股定理,可求AE和⊙O的半径的长,然后证明ΔABE∽ΔADP,利用相似三角形的性质可得DP=
的中点时,DP是⊙O的切线,因为DP∥BC,所以只需要证明PA⊥BC,可得DP⊥PA,而在△ABC中利用三线合一可证PA⊥BC;(2)连接OB,设PA交BC于点E.在RtΔABE和RtΔOBE中,由勾股定理,可求AE和⊙O的半径的长,然后证明ΔABE∽ΔADP,利用相似三角形的性质可得DP=![]() .
.
试题解析:解:(1)当点P是![]() 的中点时,DP是⊙O的切线. (1分)
的中点时,DP是⊙O的切线. (1分)
理由如下:
连接AP,∵AB=AC,∴![]() =
=![]() .
.
又∵![]() =
=![]() ,∴
,∴![]() =
=![]() .
.
∴PA是⊙O的直径. (2分)
∵![]() =
=![]() ,∴∠1=∠2.
,∴∠1=∠2.
又∵AB=AC,∴PA⊥BC. (3分)
又∵DP∥BC,∴DP⊥PA.
∴DP是⊙O的切线. (4分)
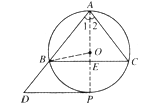
(2)连接OB,设PA交BC于点E.
由垂径定理,得BE=EC=6. (5分)
在RtΔABE中,由勾股定理,
得AE=![]() =
=![]() =8. (6分)
=8. (6分)
设⊙O的半径为r,则OE=8-r,
在RtΔOBE中,由勾股定理,
得![]() ,解得r=
,解得r=![]() . (8分)
. (8分)
∵DP∥BC,∴∠ABE=∠D.
又∵∠1=∠1,∴ΔABE∽ΔADP,
∴![]() ,即
,即 ,解得DP=
,解得DP=![]() . (10分)
. (10分)

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目