题目内容
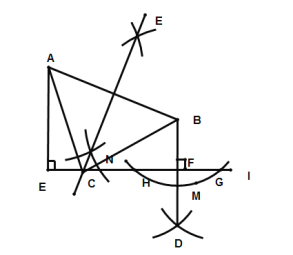
【题目】如图,已知点A、B以及直线l,AE⊥l,垂足为点E.
(1)尺规作图:①过点B作BF⊥l,垂足为点F
②在直线l上求作一点C,使CA=CB;(要求:在图中标明相应字母,保留作图痕迹,不写作法)
(2)在所作的图中,连接CA、CB,若∠ACB=90°,∠CAE=![]() ,则∠CBF= (用含
,则∠CBF= (用含![]() 的代数式表示)
的代数式表示)

【答案】(1)见详解;(2)见详解;(3)![]()
【解析】
(1)1、在直线l外关于点B的另一侧任意取点M;2、以B为圆心,AM的长为半径作弧交l于H、G; 3、分别以H、G为圆心,大于![]() 的长为半径作弧,两弧相交于点D;4、作直线BD,交直线l与点F,直线BF即为所求;
的长为半径作弧,两弧相交于点D;4、作直线BD,交直线l与点F,直线BF即为所求;
(2)1、连接AB,分别以A、B为圆心,大于![]() 的长为半径作弧,两弧相交于点E、N;2、作直线EN,交直线l与点C,点C即为所求;
的长为半径作弧,两弧相交于点E、N;2、作直线EN,交直线l与点C,点C即为所求;
(3)根据互余求解即可.
解:(1)如图,直线BF即为所求;
(2)如图,点C即为所求;
(3)∵![]()
∴![]()
∴![]()
∵∠CAE=![]()
∴![]()
故答案为:![]() .
.

练习册系列答案
相关题目









