Question

【题目】如图，在平面直角坐标系xOy中，菱形OABC的顶点A的坐标为(5，0)，顶点B、C都在第一象限，对角线AC、BO交于点D，双曲线y=（x＞0）经过点D，且ACBO40，则k的值为（ ）

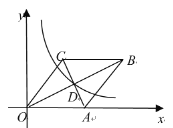
A.6B.8C.10D.12

Answer 1

【答案】B

【解析】

首先过点D作DE⊥x轴于点E，由菱形OABC中，ACOB=40，可求得菱形OABC的面积，继而求得△AOD的面积，则可求得高DE，然后由△ODE∽△DAE，可得DE2=OEAE，继而求得答案．

过点D作DE⊥x轴于点E，

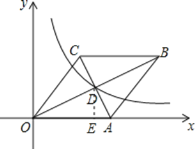
∵菱形OABC中，ACBO=40，

∴S菱形OABC=ACBO=20，

∴S△OAD=S菱形OABC=5，

∵S△OAD=OADE，且OA=5，

∴DE=2，

∵四边形OABC是菱形，

∴,即∠ADO=90°,

∴∠ODE+∠ADE=90°，

∵∠DOE+∠ODE=90°,

∴∠DOE=∠ADE，

∵∠DEA=∠DEO=90°

∴△ODE∽△DAE

∴

∴DE2=OEAE=4，OE+AE=5，

∴OE=4，AE=1，

∴点D（4，2），

∴k=4×2=8．

故选：B．