题目内容
【题目】已知∠AOB=α(90°<α<180°),∠COD在∠AOB的内部,OM平分∠AOC,ON平分∠BOD. 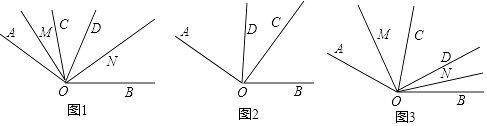
(1)若∠COD=180°﹣α时,探索下面两个问题: ①如图1,当OC在OD左侧,求∠MON的度数;
②当OC在OD右侧,请在图2内补全图形,并求出∠MON的度数(用含α的代数式表示);
(2)如图3,当∠COD=kα,且OC在OD左侧时,直接写出∠MON的度数(用含α、k的代数式表示).
【答案】
(1)解:①如图1,

∵OM平分∠AOC,ON平分∠BOD,
∴∠AOM= ![]() ∠AOC,∠BON=
∠AOC,∠BON= ![]() ∠BOD,
∠BOD,
∴∠AOM+∠BON= ![]() (∠AOC+∠BOD),
(∠AOC+∠BOD),
∵∠AOB=α,∠COD=180°﹣α,
∴∠AOC+∠BOD=∠AOB﹣∠COD=α﹣(180°﹣α)=2α﹣180°,
∴∠AOM+∠BON= ![]() (2α﹣180°)=α﹣90°,
(2α﹣180°)=α﹣90°,
∴∠MON=∠AOB﹣(∠AOM+∠BON)=α﹣(α﹣90°)=90°
②当OC在OD右侧,补全图形如图2所画,

∵OM平分∠AOC,ON平分∠BOD,
∴∠AOM= ![]() ∠AOC,∠BON=
∠AOC,∠BON= ![]() ∠BOD,
∠BOD,
∵∠AOB=α,∠COD=180°﹣α,
∴∠AOC+∠BOD=∠AOB+∠COD=α+(180°﹣α)=180°,
∴∠AOM+∠BON= ![]() ×180°=90°,
×180°=90°,
∴∠MON=∠AOB﹣(∠AOM+∠BON)=α﹣90°
(2)解:∠MON的度数为 ![]() (1+k)α.
(1+k)α.
理由:如图3,
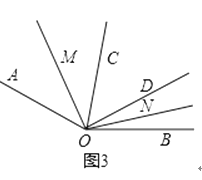
∵OM平分∠AOC,ON平分∠BOD,
∴∠AOM= ![]() ∠AOC,∠BON=
∠AOC,∠BON= ![]() ∠BOD,
∠BOD,
∴∠AOM+∠BON= ![]() (∠AOC+∠BOD),
(∠AOC+∠BOD),
∵∠AOB=α,∠COD=kα,
∴∠AOC+∠BOD=∠AOB﹣∠COD=α﹣kα,
∴∠AOM+∠BON= ![]() (α﹣kα)=
(α﹣kα)= ![]() α(1﹣k),
α(1﹣k),
∴∠MON=∠AOB﹣(∠AOM+∠BON)=α﹣ ![]() α(1﹣k)=
α(1﹣k)= ![]() (1+k)α
(1+k)α
【解析】(1)①根据角平分线的定义,得出∠AOM= ![]() ∠AOC,∠BON=
∠AOC,∠BON= ![]() ∠BOD,再根据∠AOB=α,∠COD=180°﹣α,得出∠AOC+∠BOD=∠AOB﹣∠COD=α﹣(180°﹣α)=2α﹣180°,进而得出∠AOM+∠BON=
∠BOD,再根据∠AOB=α,∠COD=180°﹣α,得出∠AOC+∠BOD=∠AOB﹣∠COD=α﹣(180°﹣α)=2α﹣180°,进而得出∠AOM+∠BON= ![]() (2α﹣180°)=α﹣90°,最后根据∠MON=∠AOB﹣(∠AOM+∠BON)进行计算即可;②根据①中的方法进行计算,即可得出∠MON的度数;(2)先根据角平分线的定义,得出∠AOM=
(2α﹣180°)=α﹣90°,最后根据∠MON=∠AOB﹣(∠AOM+∠BON)进行计算即可;②根据①中的方法进行计算,即可得出∠MON的度数;(2)先根据角平分线的定义,得出∠AOM= ![]() ∠AOC,∠BON=
∠AOC,∠BON= ![]() ∠BOD,再根据∠AOB=α,∠COD=kα,得出∠AOC+∠BOD=∠AOB﹣∠COD=α﹣kα,进而得到∠AOM+∠BON=
∠BOD,再根据∠AOB=α,∠COD=kα,得出∠AOC+∠BOD=∠AOB﹣∠COD=α﹣kα,进而得到∠AOM+∠BON= ![]() (α﹣kα)=
(α﹣kα)= ![]() α(1﹣k),最后根据∠MON=∠AOB﹣(∠AOM+∠BON)进行计算即可.
α(1﹣k),最后根据∠MON=∠AOB﹣(∠AOM+∠BON)进行计算即可.
【考点精析】解答此题的关键在于理解角的平分线的相关知识,掌握从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线,以及对角的运算的理解,了解角之间可以进行加减运算;一个角可以用其他角的和或差来表示.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案