题目内容
【题目】如图,在平面直角坐标系xOy中,直线y=kx﹣3与双曲线![]() 的两个交点为A,B,其中A(﹣1,m).
的两个交点为A,B,其中A(﹣1,m).
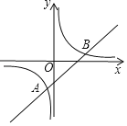
(1)求m的值及直线的表达式;
(2)若点M为x轴上一个动点,且△AMB为直角三角形,直接写出满足条件的点M的个数.
【答案】(1)m=﹣4,y=x﹣3;(2)点M有4个
【解析】
(1)先利用待定系数法求出点A坐标,进而代入双曲线解析式中即可得出结论;
(2)先求出点B的坐标,分三种情况,用勾股定理建立方程即可求出结论.
解:(1)把A(﹣1,m)代入![]() 得
得
∴m=﹣4
把A(﹣1,﹣4)代入y=kx﹣3
∴﹣4=﹣k﹣3
∴k=1
∴y=x﹣3,
(2)由(1)知,直线AB的解析式为y=x﹣3①,
∵双曲线的解析式为![]() ②,
②,
联立①②解得,![]() 或
或![]() ,
,
∴A(﹣1,﹣4),B(4,1),
设点M的坐标为(m,0),
∴AB2=50,AM2=(m+1)2+16,BM2=(m﹣4)2+1
∵△AMB是直角三角形,
∴①当∠AMB=90°时,AM2+BM2=AB2,
∴50=(m+1)2+16+(m﹣4)2+1,
∴![]() ,
,
∴M(![]() ,0)或(
,0)或(![]() ,0);
,0);
②当∠BAM=90°时,AB2+AM2=BM2,
∴50+(m+1)2+16=(m﹣4)2+1,
∴m=﹣5,
∴M(﹣5,0);
③当∠ABM=90°时,AB2+BM2=AM2,
∴50+(m﹣4)2+1=(m+1)2+16,
∴m=5,
∴M(5,0)
∴满足条件的点M有4个.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
【题目】为了帮助市内一名患“白血病”的中学生,东营市某学校数学社团15名同学积极捐款,捐款情况如下表所示,下列说法正确的是( )
捐款数额 | 10 | 20 | 30 | 50 | 100 |
人数 | 2 | 4 | 5 | 3 | 1 |
A. 众数是100 B. 中位数是30 C. 极差是20 D. 平均数是30