题目内容
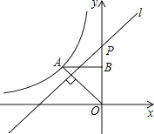
【题目】如图,直线![]() ,点
,点![]() 是
是![]() 、
、![]() 之间(不在直线
之间(不在直线![]() ,
,![]() 上)的一个动点,
上)的一个动点,
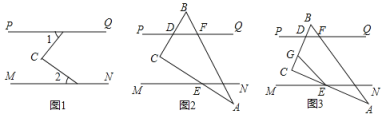
(1)若![]() 与
与![]() 都是锐角,如图1,请直接写出
都是锐角,如图1,请直接写出![]() 与
与![]() ,
,![]() 之间的数量关系;
之间的数量关系;
(2)若把一块三角尺(![]() ,
,![]() )按如图2方式放置,点
)按如图2方式放置,点![]() ,
,![]() ,
,![]() 是三角尺的边与平行线的交点,若
是三角尺的边与平行线的交点,若![]() ,求
,求![]() 的度数;
的度数;
(3)将图乙中的三角尺进行适当转动,如图3,直角顶点![]() 始终在两条平行线之间,点
始终在两条平行线之间,点![]() 在线段
在线段![]() 上,连接
上,连接![]() ,且有
,且有![]() ,求
,求![]() 的值.
的值.
【答案】(1)∠C=∠1+∠2;(2)60°;(3)2
【解析】
(1)过点C作CF//PQ,可证明CF//PQ//MN,再根据两直线平行内错角相等即可证明;
(2)根据(1)的结论及∠A的度数即可求出∠BDF的度数;
(3) 设∠CEM=α,则∠GEN=180°2α,∠BDF=∠PDC =90°α,即可求出![]() 的值.
的值.
解:(1)∠C=∠1+∠2.
理由如下:如图,
过点C作CF//PQ,
∵PQ//CF,
∴∠1=∠ACF,
∵PQ//MN,
∴CF//MN,
∴∠2=∠FCB,
∵∠C=∠ACF+∠FCB,
∴∠C=∠1+∠2;
(2)∵∠AEN=∠A=30°,∠C=90°,
∴由(1)可得∠PDC=60°,
∴∠BDF=∠PDC=60°;
(3)设∠CEM=α,则有∠GEN=180°2α,∠BDF=∠PDC=90°α,
∴![]() =
=![]() .
.

【题目】学校准备从甲乙两位选手中选择一位选手代表学校参加所在地区的汉字听写大赛,学校对两位选手从表达能力、阅读理解、综合素质和汉字听写四个方面做了测试,他们各自的成绩(百分制)如表:
选手 | 表达能力 | 阅读理解 | 综合素质 | 汉字听写 |
甲 | 85 | 78 | 85 | 73 |
乙 | 73 | 80 | 82 | 83 |
(1)由表中成绩已算得甲的平均成绩为80.25,请计算乙的平均成绩,从他们的这一成绩看,应选派谁;
(2)如果表达能力、阅读理解、综合素质和汉字听写分别赋予它们2、1、3和4的权,请分别计算两名选手的平均成绩,从他们的这一成绩看,应选派谁.
【题目】养成良好的早锻炼习惯,对学生的学习和生活非常有益![]() 某中学为了了解七年级学生的早锻炼情况,校政教处在七年级随机抽取了部分学生,并对这些学生通常情况下一天的早锻炼时间
某中学为了了解七年级学生的早锻炼情况,校政教处在七年级随机抽取了部分学生,并对这些学生通常情况下一天的早锻炼时间![]() 分钟
分钟![]() 进行了调查
进行了调查![]() 现把调查结果分为A,B,C,D四组,如下表所示;同时,将调查结果绘制成下面两幅不完整的统计图.
现把调查结果分为A,B,C,D四组,如下表所示;同时,将调查结果绘制成下面两幅不完整的统计图.
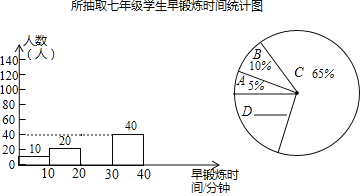
组别 | 早锻炼时间 |
A |
|
B |
|
C |
|
D |
|
请根据以上提供的信息,解答下列问题:
![]() 扇形统计图中D所在扇形的圆心角度数为______;
扇形统计图中D所在扇形的圆心角度数为______;
![]() 补全频数分布直方图;
补全频数分布直方图;
![]() 已知该校七年级共有1200名学生,请你估计这个年级学生中有多少人一天早锻炼的时间不少于20分钟.
已知该校七年级共有1200名学生,请你估计这个年级学生中有多少人一天早锻炼的时间不少于20分钟.