题目内容
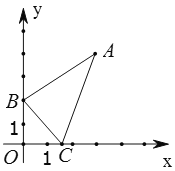
【题目】如图,在平面直角坐标系中,已知![]() 、
、![]() ,在
,在![]() 轴上有一动点
轴上有一动点![]() ,当
,当![]() 的周长最小时,则点
的周长最小时,则点![]() 的坐标为_____.
的坐标为_____.
【答案】(1,0)
【解析】
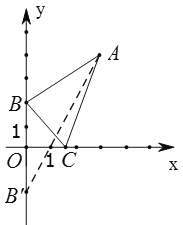
先作出点B关于x轴的对称点B′,连接AB′交x轴于点C,再用待定系数法求出过AB′两点的一次函数解析式,求出此函数与x轴的交点坐标即可.
先作出B关于x轴的对称点B′,连接AB′交x轴于点C,则B点坐标为(0,2),
由两点之间线段最短可知,AB′的长即为AC+BC的长,
因为AB是定值,
所以此时△ABC的周长最小,
设过AB′两点的一次函数解析式为y=kx+b(k≠0),则
![]() ,
,
解得k=2,b=2,
故此一次函数的解析式为y=2x2,
当y=0时,2x2=0,解得x=1.
故C(1,0)时,△ABC的周长最短.
故答案为:(1,0).

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
【题目】养成良好的早锻炼习惯,对学生的学习和生活非常有益![]() 某中学为了了解七年级学生的早锻炼情况,校政教处在七年级随机抽取了部分学生,并对这些学生通常情况下一天的早锻炼时间
某中学为了了解七年级学生的早锻炼情况,校政教处在七年级随机抽取了部分学生,并对这些学生通常情况下一天的早锻炼时间![]() 分钟
分钟![]() 进行了调查
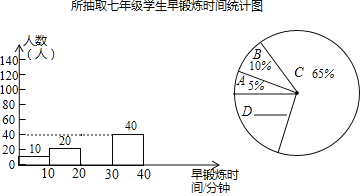
进行了调查![]() 现把调查结果分为A,B,C,D四组,如下表所示;同时,将调查结果绘制成下面两幅不完整的统计图.
现把调查结果分为A,B,C,D四组,如下表所示;同时,将调查结果绘制成下面两幅不完整的统计图.
组别 | 早锻炼时间 |
A |
|
B |
|
C |
|
D |
|
请根据以上提供的信息,解答下列问题:
![]() 扇形统计图中D所在扇形的圆心角度数为______;
扇形统计图中D所在扇形的圆心角度数为______;
![]() 补全频数分布直方图;
补全频数分布直方图;
![]() 已知该校七年级共有1200名学生,请你估计这个年级学生中有多少人一天早锻炼的时间不少于20分钟.
已知该校七年级共有1200名学生,请你估计这个年级学生中有多少人一天早锻炼的时间不少于20分钟.