题目内容
如果10b=n,那么b为n的劳格数,记为b=d(n),由定义可知:10b=n与b=d(n)所表示的b、n两个量之间的同一关系.
(1)根据劳格数的定义,填空:d(10)= ,d(10-2)= ;
(2)劳格数有如下运算性质:
若m、n为正数,则d(mn)=d(m)+d(n),d(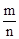 )=d(m)-d(n).
)=d(m)-d(n).
根据运算性质,填空: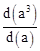 = (a为正数),若d(2)=0.3010,则d(4)= ,d(5)= ,d(0.08)= ;
= (a为正数),若d(2)=0.3010,则d(4)= ,d(5)= ,d(0.08)= ;
(3)如表中与数x对应的劳格数d(x)有且只有两个是错误的,请找出错误的劳格数,说明理由并改正.
(1)根据劳格数的定义,填空:d(10)= ,d(10-2)= ;
(2)劳格数有如下运算性质:
若m、n为正数,则d(mn)=d(m)+d(n),d(
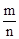 )=d(m)-d(n).
)=d(m)-d(n).根据运算性质,填空:
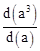 = (a为正数),若d(2)=0.3010,则d(4)= ,d(5)= ,d(0.08)= ;
= (a为正数),若d(2)=0.3010,则d(4)= ,d(5)= ,d(0.08)= ;(3)如表中与数x对应的劳格数d(x)有且只有两个是错误的,请找出错误的劳格数,说明理由并改正.
| x | 1.5 | 3 | 5 | 6 | 8 | 9 | 12 | 27 |
| d(x) | 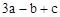 | 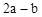 |  |  |  | 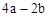 |  |  |
解:(1)1,﹣2。
(2)3;0.6020;0.6990;﹣1.097。
(3)表中只有d(1.5)和d(12)的值是错误的,应纠正为:
 ,
,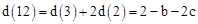 。
。
(2)3;0.6020;0.6990;﹣1.097。
(3)表中只有d(1.5)和d(12)的值是错误的,应纠正为:
 ,
,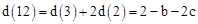 。
。分析:(1)根据定义可知,10b=n与b=d(n)所表示的b、n两个量之间的同一关系,d(10)和d(10﹣2)就是指10的指数,所以d(10)=1,d(10﹣2)=-2。
(2)根据d(a3)=d(a•a•a)=d(a)+d(a)+d(a)即可求得
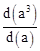 的值;根据d(4)="2" d(2),d(5)= d(
的值;根据d(4)="2" d(2),d(5)= d(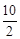 )= d(10)-d(2)= 1-d(2),d(0.08)= d(10-2×23)=―2+3 d(2)可求解。
)= d(10)-d(2)= 1-d(2),d(0.08)= d(10-2×23)=―2+3 d(2)可求解。(3)通过9=32,27=33,可以判断d(3)是否正确,同理以依据5=10÷2,假设d(5)正确,可以求得d(2)的值,即可通过d(8),d(12)作出判断。
解:(1)1,﹣2。
(2)3;0.6020;0.6990;﹣1.097。
(3)应用反证法:
若
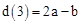 ,则
,则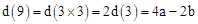 ,
,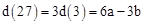 ,
,∴若
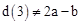 ,表中有三个劳格数是错误的,与题设矛盾。
,表中有三个劳格数是错误的,与题设矛盾。∴
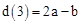 ,
, ,
,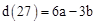 。
。若
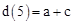 ,则
,则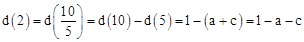 ,
,∴
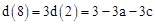 ,
,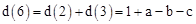 。
。∴若
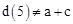 ,表中也有三个劳格数是错误的,与题设矛盾。
,表中也有三个劳格数是错误的,与题设矛盾。∴
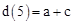 ,
,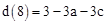 ,
, 。
。∴表中只有d(1.5)和d(12)的值是错误的,应纠正为:
 ,
,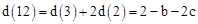 。
。
练习册系列答案
相关题目
 且
且 无意义,求
无意义,求 的值.
的值. ,其中a=﹣1.
,其中a=﹣1. =__________________.
=__________________.



 ,则代数式
,则代数式 的值为 .
的值为 . ,则
,则 的值是 。
的值是 。