Question

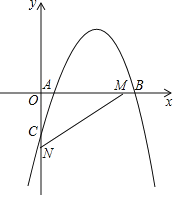
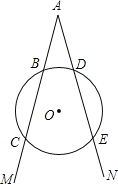
【题目】如图所示，射线AM交一圆于点B，C，射线AN交该圆于点D，F，且BC＝DE，求证：AC＝AE．

Answer 1

【答案】见解析

【解析】

作OP⊥AC于P，OQ⊥AE于Q，连接OB、OD、OA，通过证明Rt△OPB≌Rt△OQD，从而有OP＝OQ，再证明Rt△OPA≌Rt△OQA，有AP＝AQ，从而结论可证.

证明：作OP⊥AC于P，OQ⊥AE于Q，连接OB、OD、OA，则PB＝BC，DQ＝DE，

∵BC＝DE，

∴PB＝DQ，PC＝QE，

在Rt△OPB和Rt△OQD中，

∴Rt△OPB≌Rt△OQD（HL），

∴OP＝OQ，

在Rt△OPA和Rt△OQA中，

∴Rt△OPA≌Rt△OQA（HL），

∴AP＝AQ，

∴AP+PC＝AQ+QE，

即AC＝AE．