题目内容
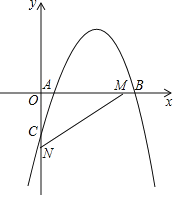
【题目】如图,平面直角坐标系中,抛物线y=﹣x2+4x+m﹣4(m为常数)与y轴的交点为C,M(3,0)与N(0,﹣2)分别是x轴、y轴上的点
(1)当m=1时,求抛物线顶点坐标.
(2)若3≤x≤3+m时,函数y=﹣x2+4x+m﹣4有最小值﹣7,求m的值.
(3)若抛物线与线段MN有公共点,直接写出m的取值范围是 .
【答案】(1)顶点坐标为(2,1);(2)m=2;(3)﹣![]() ≤m≤2.
≤m≤2.
【解析】
(1)利用配方法求顶点的坐标;
(2)根据二次函数的性质得到当x=m+3时,y有最小值﹣7,即可得到﹣(m+3)2+4(m+3)+m﹣4=﹣7,求解即可;
(3)求得直线MN的解析式,然后根据题意得到(﹣![]() )2﹣4(﹣m+2)≥0且m﹣4≤﹣2,求解即可.
)2﹣4(﹣m+2)≥0且m﹣4≤﹣2,求解即可.
解:(1)当m=1时,y=﹣x2+4x﹣3=﹣(x﹣2)2+1,
∴顶点坐标为(2,1);
(2)由题意可知,该抛物线开口向下,对称轴为直线x=![]() =2,
=2,
∴当3≤x≤3+m时,y随x的增大而减小,
∴当x=m+3时,y取最小值﹣7,
∴﹣(m+3)2+4(m+3)+m﹣4=﹣7,
解得:m1=2,m2=﹣3(舍去),
∴m=2;
(3)∵M(3,0),N(0,﹣2),
设直线MN解析式为:y=kx+b(k≠0),
则![]() ,解得:
,解得: ,
,
∴直线MN的解析式为y=![]() x﹣2,
x﹣2,
∵抛物线与线段MN有公共点,则方程﹣x2+4x+m﹣4=![]() x﹣2,即x2﹣
x﹣2,即x2﹣![]() x﹣m+2=0中△≥0,且m﹣4≤﹣2,
x﹣m+2=0中△≥0,且m﹣4≤﹣2,
∴(﹣![]() )2﹣4(﹣m+2)≥0,
)2﹣4(﹣m+2)≥0,
解得:﹣![]() ≤m≤2,
≤m≤2,
故答案为:﹣![]() ≤m≤2.
≤m≤2.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目