题目内容
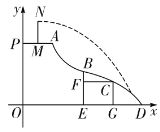
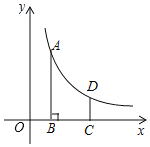
【题目】如图，反比例函数y＝
（x＞0）的图象上一点A（m，4），过点A作AB⊥x轴于B，CD∥AB，交x轴于C，交反比例函数图象于D，BC＝2，CD＝
．
（1）求反比例函数的表达式；
（2）若点P是y轴上一动点，求PA+PB的最小值．
【答案】（1）
；（2）2
【解析】
（1）可得点D的坐标为：
，点A（m，4），即可得方程4m=
（m+2），继而求得答案；
（2）作点A关于y轴的对称点E，连接BF交y轴于点P，可求出BF长即可．
解：（1）∵CD∥y轴，CD＝，
∴点D的坐标为：（m+2，），
∵A，D在反比例函数y＝
（x＞0）的图象上，
∴4m＝（m+2），
解得：m＝1，
∴点A的坐标为（1，4），
∴k＝4m＝4，
∴反比例函数的解析式为：y＝
；
（2）过点A作AE⊥y轴于点E，并延长AE到F，使AE＝FE＝1，连接BF交y轴于点P，则PA+PB的值最小．
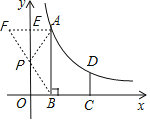
∴PA+PB＝PF+PB＝BF＝
．
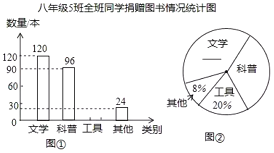
【题目】为弘扬中华优秀传统文化，某校组织了“古诗词”知识竞赛，由九年级的若干名学生参加选拔赛，从中选出10名优胜者，下面是对参赛学生成绩的不完整统计．
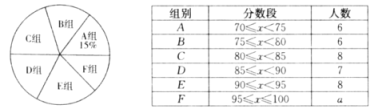
（1）统计表中，
=_____；各组人数的中位数是_____；统计图中，
组所在扇形的圆心角是_____°；
（2）李明同学得了88分，他说自己在参加选拔赛的同学中属于中午偏上水平，你认为他说的有道理吗？为什么？
（3）选出的10名优胜者中，男生、女生的分布情况如下表．
一班 | 二班 | 三班 | 四班 | 五班 | 六班 | |
男生人数 | 1 | 1 | 2 | 1 | 0 | 0 |
女生人数 | 1 | 0 | 0 | 2 | 1 | 1 |
若从中任选1名男生和1名女生代表学校参加全区的比赛，请有列表法或画树状图法求男生和女生都出在四班的概率．
【题目】丁老师为了解所任教的两个班的学生数学学习情况，对数学进行了一次测试，获得了两个班的成绩（百分制），并对数据（成绩）进行整理、描述和分析，下面给出了部分信息．①A、B两班学生（两个班的人数相同）数学成绩不完整的频数分布直方图如下（数据分成 5 组：x＜60，60≤x＜70，70≤x＜80，80≤x＜90，90≤x≤100）：
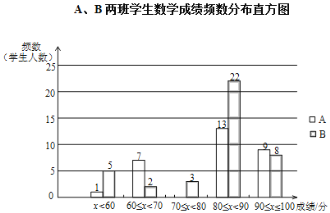
②A、B两班学生测试成绩在80≤x＜90这一组的数据如下：
A 班：80 80 82 83 85 85 86 87 87 87 88 89 89
B 班：80 80 81 81 82 82 83 84 84 85 85 86 86 86 87 87 87 87 87 88 88 89
③A、B两班学生测试成绩的平均数、中位数、方差如下：
平均数 | 中位数 | 方差 | |
A班 | 80.6 | m | 96.9 |
B班 | 80.8 | n | 153.3 |
根据以上信息，请写出表中 m、n的值____________．
