题目内容
【题目】如图，在等腰三角形ABC中，∠BAC=90°，AB=AC=1，BD平方∠ABC，点P在BD上，⊙P切AB于点Q，则AP+PQ的最小值等于 ．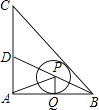 
【答案】
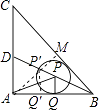
【解析】解：如图，过点A作AM⊥BC于点M，交BD于点P′，过点P′作P′Q′⊥AB于点Q′，
∵BD平分∠ABC．
∴P′Q′=P′M，这时AP′+P′Q′有最小值，即AM的长度，
∴当P和P′重合时，AP+PQ的最小值就是AM的长，
∵AB=AC=1，∠BAC=90°，
∴BC= 
= 
．
∵△ABC是等腰直角三角形，
∴AM是直角三角形斜边的中线，
∴AM= 
BC=
即PC+PQ的最小值为 ，
所以答案是 ．
【考点精析】本题主要考查了切线的性质定理的相关知识点，需要掌握切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能正确解答此题．
练习册系列答案
阅读快车系列答案
相关题目
【题目】某学校的复印任务原来由甲复印社承接，其收费y（元）与复印页数x（页）的关系如下表：
x（页） | 100 | 200 | 400 | 1000 | … |
y（元） | 40 | 80 | 160 | 400 |
（1）若y与x满足初中学过的某一函数关系，求函数的解析式；
（2）现在乙复印社表示：若学校先按每月付给200元的承包费，则可按每页0.15元收费．则乙复印社每月收费y（元）与复印页数x（页）的函数关系为 ；
（3）应选择哪个复印社比较优惠？
