题目内容
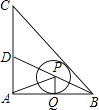
【题目】如图,在ABCD中,O为对角线AC的中点,EF经过点O并与AB,CD分别相交于点E,F.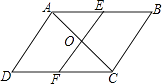
(1)求证:AE=CF;
(2)当EF⊥AC时,连接AF,CE,试判断四边形AFCE是怎样的四边形?并证明你的结论.
【答案】
(1)
证明:∵四边形ABCD是平行四边形,
∴AB∥CD,∴∠EAO=∠FCO,
∵O为AC的中点,
∴OA=OC,
在△AOE和△COF中, 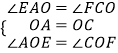 ,
,
∴△AOE≌△COF(ASA),
∴AE=CF;
(2)
解:如图所示:四边形AFCE是菱形;
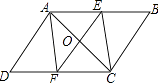
理由如下:
由(1)得:△AOE≌△COF,
∴OE=OF,
∵OA=OC,
∴四边形AFCE是平行四边形,
又∵EF⊥AC,
∴四边形AFCE是菱形.
【解析】(1)由ASA证明△AOE≌△COF,的长对应边相等即可;(2)先由对角线互相平分证出四边形AFCE是平行四边形,再由EF⊥AC,即可证出四边形AFCE是菱形.
【考点精析】解答此题的关键在于理解平行四边形的性质的相关知识,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分,以及对菱形的判定方法的理解,了解任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形.

【题目】某学校有1500名学生参加首届“我爱我们的课堂”为主题的图片制作比赛,赛后随机抽取部分参赛学生的成绩进行整理并制作成图表如图:
分数段 | 频数 | 频率 |
60≤x<70 | 40 | 0.40 |
70≤x<80 | 35 | b |
80≤x<90 | a | 0.15 |
90≤x<100 | 10 | 0.10 |
频率分布统计表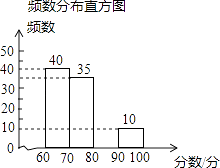
请根据上述信息,解答下列问题:
(1)分别求出a、b的值;
(2)请补全频数分布直方图;
(3)如果将比赛成绩80分以上(含80分)定为优秀,那么优秀率是多少?并且估算该校参赛学生获得优秀的人数.
【题目】为了让同学们了解自己的体育水平,初二1班的体育刘老师对全班45名学生进行了一次体育模拟测试(得分均为整数),成绩满分为10分,1班的体育委员根据这次测试成绩,制作了统计图和分析表如下:
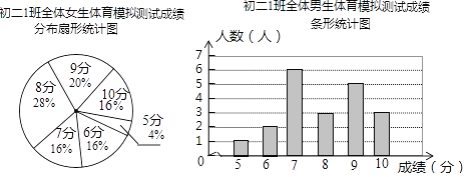
初二1班体育模拟测试成绩分析表
平均分 | 方差 | 中位数 | 众数 | |
男生 | 2 | 8 | 7 | |
女生 | 7.92 | 1.99 | 8 |
根据以上信息,解答下列问题:
(1)这个班共有男生________人,共有女生________人;
(2)补全初二1班体育模拟测试成绩分析表.