题目内容
【题目】已知O为直线AB上一点,∠COE为直角,OF平分∠AOE.
(1)如图1,若∠COF=30°,则∠BOE=_______;若∠COF=m°,则∠BOE=_______,∠BOE和∠COF的数量关系为___________;
(2)当射线OE绕点O逆时针旋转到图2的位置时,(1)中∠BOE和∠COF的数量关系是否仍成立?请说明理由.
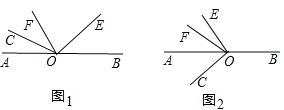
【答案】(1)60°;2m°;∠BOE=2∠COF;(2)∠BOE=2∠COF仍成立.理由见解析.
【解析】
(1)当∠COF= m°,根据弧余得到∠EOF=90°- m°,再由OF平分∠AOE,得到∠AOE=2∠EOF=180°-2 m°,然后根据邻补角的定义得到∠BOE=180°-(180°-2 m°)=2 m°,所以有∠BOE=2∠COF.并且当n=34°时,可求出对应的∠BOE;
(2)和(1)推论得方法一样,可得到∠BOE=2∠COF.
(1) ∵∠COE是直角,∠COF=30°,
∴∠EOF=90°-30°=60°,
由∵OF平分∠AOE.
∴∠AOE=2∠EOF=120°,
∴∠BOE=180°-120°=60°;
当∠COF= m°,
∴∠EOF=90°- m°,
∴∠AOE=2∠EOF=180°-2 m°,
∴∠BOE=180°-(180°-2 m°)=2 m°,
所以有∠BOE=2∠COF,
故答案为:60°;2m°;∠BOE=2∠COF;
(2)∠BOE=2∠COF仍成立,
设∠COF=n°,
∵∠COE是直角,
∴∠EOF=90°-n°,
又∵OF平分∠AOE,
∴∠AOE=2∠EOF=180°-2n°,
∴∠BOE=180°-(180°-2n°)=2n°,
即∠BOE=2∠COF.

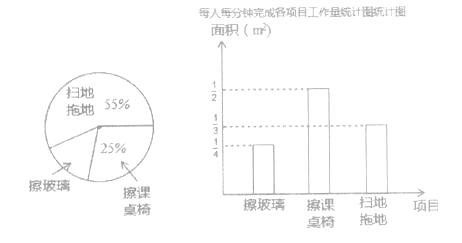
【题目】为了让同学们了解自己的体育水平,初二1班的体育刘老师对全班45名学生进行了一次体育模拟测试(得分均为整数),成绩满分为10分,1班的体育委员根据这次测试成绩,制作了统计图和分析表如下:
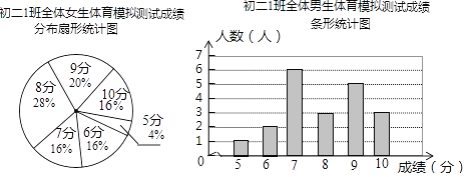
初二1班体育模拟测试成绩分析表
平均分 | 方差 | 中位数 | 众数 | |
男生 | 2 | 8 | 7 | |
女生 | 7.92 | 1.99 | 8 |
根据以上信息,解答下列问题:
(1)这个班共有男生________人,共有女生________人;
(2)补全初二1班体育模拟测试成绩分析表.