题目内容
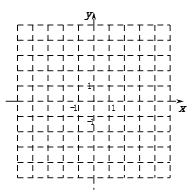
【题目】如图,数轴上,点A的初始位置表示的数为1,现点A做如下移动:第1次点A向左移动3个单位长度至点A1,第2次从点A1向右移动6个单位长度至点A2,第3次从点A2向左移动9个单位长度至点A3,…,按照这种移动方式进行下去,点A2019表示的数,是______.
![]()
【答案】-3029
【解析】
序号为奇数的点在点A的左边,各点所表示的数依次减少3,序号为偶数的点在点A的右侧,各点所表示的数依次增加3,依次找出规律。
解:第一次点A向左移动3个单位长度至点A1,则A1表示的数,1-3=-2;
第2次从点A1向右移动6个单位长度至点A2,则A2表示的数为-2+6=4;
第3次从点A2向左移动9个单位长度至点A3,则A3表示的数为4-9=-5;
第4次从点A3向右移动12个单位长度至点A4,则A4表示的数为-5+12=7;
第5次从点A4向左移动15个单位长度至点A5,则A5表示的数为7-15=-8;
第6次从点A5向左移动18个单位长度至点A6,则A6表示的数为-8+18=10;
…;
所以点A1=-2,A3=-5,A5=-8,…构成以2为首项,以-3为公差的等差数列;
A2=4,A4=7,A6=10,…构成以4为首项,以3为公差的等差数列;
由于(2019+1)÷2=1010,当n=2019时,这个点表示的数是:-2+(1010-1)×(-3)=-3029
故本题的答案为:-3029

【题目】随着人们生活水平的提高,家用轿车越来越多地进入家庭.小明家中买了一辆小轿车,他连续记录了7天中每天行驶的路程(如表),以50km为标准,多于50km的记为“+”,不足50km的记为“﹣”,刚好50km的记为“0”.
第一天 | 第二天 | 第三天 | 第四天 | 第五天 | 第六天 | 第七天 | |
路程(km) | ﹣8 | ﹣11 | ﹣14 | 0 | ﹣16 | +41 | +8 |
(1)请求出这七天平均每天行驶多少千米;
(2)若每行驶100km需用汽油6升,汽油价6.2元/升,请估计小明家一个月(按30天计)的汽油费用是多少元?