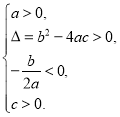题目内容
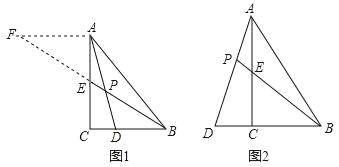
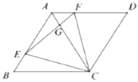
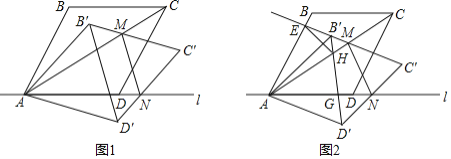
【题目】图1,菱形ABCD的顶点A,D在直线上,∠BAD=60°,以点A为旋转中心将菱形ABCD顺时针旋转α(0°<α<30°),得到菱形AB′C′D′,B′C′交对角线AC于点M,C′D′交直线l于点N,连接MN.
(1)当MN∥B′D′时,求α的大小.
(2)如图2,对角线B′D′交AC于点H,交直线l与点G,延长C′B′交AB于点E,连接EH.当△HEB′的周长为2时,求菱形ABCD的周长.
【答案】(1)15°;(2)8.
【解析】
(1)四边形AB′C′D′有一个角为60°的菱形,MN∥B′C′,可以得到△AB′D′,△B′C′D′都是等边三角形,可证得△AB′M≌△AD′N(SAS),由∠CAD=![]() ∠BAD=30°,即可求得答案;
∠BAD=30°,即可求得答案;
(2)在△A![]() E和△A
E和△A![]() G中,∠A
G中,∠A![]() E=∠A
E=∠A![]() G=60°, ∠EA
G=60°, ∠EA![]() =∠GA
=∠GA![]() =α,A
=α,A![]() =A
=A![]() ,可证得△AEB′≌△AGD′(AAS),还可以证得△AHE≌△AHG(SAS),得到B′D′=2,继而求得答案.
,可证得△AEB′≌△AGD′(AAS),还可以证得△AHE≌△AHG(SAS),得到B′D′=2,继而求得答案.
(1)∵四边形AB′C′D′是菱形,
∴AB′=B′C′=C′D′=AD′,
∵∠B′AD′=∠B′C′D′=60°,
∴△AB′D′,△B′C′D′是等边三角形,
∵MN∥B′C′,
∴∠C′MN=∠C′B′D′=60°,∠CNM=∠C′D′B′=60°,
∴△C′MN是等边三角形,
∴C′M=C′N,
∴MB′=ND′,
∵∠AB′M=∠AD′N=120°,AB′=AD′,
∴△AB′M≌△AD′N(SAS),
∴∠B′AM=∠D′AN,
∵∠CAD=![]() ∠BAD=30°,
∠BAD=30°,
∴∠DAD′=15°,
∴α=15°.
(2)在△AB`E和△AD`G中,∠AB`E=∠AD`G,∠EAB`=∠GAD`,AB`=AD`
∴△AEB′≌△AGD′(AAS),
∴EB′=GD′,AE=AG,
∵AH=AH,∠HAE=∠HAG,
∴△AHE≌△AHG(SAS),
∴EH=GH,
∵△EHB′的周长为2,
∴EH+EB′+HB′=B′H+HG+GD′=B′D′=2,
∴AB′=AB=2,
∴菱形ABCD的周长为8.

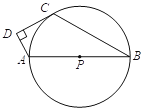
【题目】关于x 的一元二次方程a x2 + bx + c = 0(a>0)有两个不相等且非零的实数根,探究a,b,c满足的条件.
小华根据学习函数的经验,认为可以从二次函数的角度看一元二次方程,下面是小华的探究过程:第一步:设一元二次方程ax2 +bx+c = 0(a>0)对应的二次函数为y = ax2 +bx +c(a>0);
第二步:借助二次函数图象,可以得到相应的一元二次方程中a,b,c满足的条件,列表如下:
方程两根的情况 | 对应的二次函数的大致图象 | a,b,c满足的条件 |
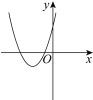
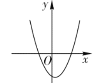
方程有两个 不相等的负实根 |
|
|
①_______ |
|
|
方程有两个 不相等的正实根 | ②__________ | ③____________ |
(1)请帮助小华将上述表格补充完整;
(2)参考小华的做法,解决问题:
若关于x的一元二次方程![]() 有一个负实根和一个正实根,且负实根大于-1,求实数
有一个负实根和一个正实根,且负实根大于-1,求实数![]() 的取值范围.
的取值范围.