题目内容
【题目】(定义[a,b,c]为函数![]() 的特征数,下面给出特征数为 [2m,1-m,-1-m]的函数的一些结论:
的特征数,下面给出特征数为 [2m,1-m,-1-m]的函数的一些结论:
①当m=-3时,函数图象的顶点坐标是(![]() ,
,![]() );
);
②当m>0时,函数图象截x轴所得的线段长度大于![]() ;
;
③当m<0时,函数在![]() 时,y随x的增大而减小;
时,y随x的增大而减小;
④当m≠0时,函数图象经过x轴上一个定点.
其中正确的结论有________ .(只需填写序号)
【答案】①②④.
【解析】
试题因为函数y=ax2+bx+c的特征数为[2m,1﹣m,﹣1﹣m];
①当m=﹣3时,y=﹣6x2+4x+2=﹣6(x﹣![]() )2+
)2+![]() ,顶点坐标是(
,顶点坐标是(![]() ,
,![]() );此结论正确;
);此结论正确;
②当m>0时,令y=0,有2mx2+(1﹣m)x+(﹣1﹣m)=0,解得x=![]() ,x1=1,x2=
,x1=1,x2=![]() ,
,
|x2﹣x1|=![]() >
>![]() ,所以当m>0时,函数图象截x轴所得的线段长度大于
,所以当m>0时,函数图象截x轴所得的线段长度大于![]() ,此结论正确;
,此结论正确;
③当m<0时,y=2mx2+(1﹣m)x+(﹣1﹣m) 是一个开口向下的抛物线,其对称轴是:![]() ,在对称轴的右边y随x的增大而减小.因为当m<0时,
,在对称轴的右边y随x的增大而减小.因为当m<0时,![]() =
=![]() >
>![]() ,即对称轴在x=
,即对称轴在x=![]() 右边,因此函数在x=
右边,因此函数在x=![]() 右边先递增到对称轴位置,再递减,此结论错误;
右边先递增到对称轴位置,再递减,此结论错误;
④当x=1时,y=2mx2+(1﹣m)x+(﹣1﹣m)=2m+(1﹣m)+(﹣1﹣m)=0 即对任意m,函数图象都经过点(1,0)那么同样的:当m=0时,函数图象都经过同一个点(1,0),当m≠0时,函数图象经过同一个点(1,0),故当m≠0时,函数图象经过x轴上一个定点此结论正确.
根据上面的分析,①②④都是正确的,③是错误的.
故答案是①②④.

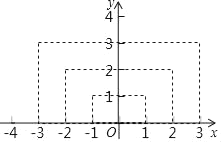
【题目】已知y是x的函数,x的取值范围为任意实数,如图是x与y的几组对应值,小华同学根据研究函数的己有经验探素这个函数的有关性质,并完成下列问题.
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | 3 | 2 | 1 | 0 | 1 | 2 | 3 | … |
(1)如图,小华在平面直角坐标系中描出了上述几组值对应的点,请你根据描出的点画出函数的图象;
(2)请根据你画出的函数图象,完成
①当x=﹣4时,求y的值;
②当2012≤|y|≤2019时,求x的取值范围.