题目内容
【题目】如图,在平面直角坐标系中,点A在第二象限且纵坐标为1,点B在x轴的负半轴上,AB=AO,∠ABO=30°,直线MN经过原点O,点A关于直线MN的对称点A1在x轴的正半轴上,点B关于直线MN的对称点为B1 . 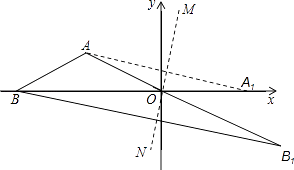
(1)求∠AOM的度数.
(2)已知30°,60°,90°的三角形三边比为1: ![]() :2,求线段AB1的长和B1的纵坐标.
:2,求线段AB1的长和B1的纵坐标.
【答案】
(1)
解:∵点A与点A1关于直线MN对称,
∴∠AOM=∠A1OM,
∵AB=AO,∠ABO=30°,
∴∠AOB=30°,
∵∠AOB+∠AOM+∠A1OM=180°,
∴∠AOM=75°
(2)
解:过点A作AC⊥x轴于点C,过点B1作B1D⊥x轴于点D,如图所示.
∵∠AOC=30°,∠ACO=90°,AC=1,
∴AO=2AC=2,OC= ![]() AC=
AC= ![]() ,
,
∵AB=AO,
∴BO=2OC=2 ![]() ,
,
∴点A(﹣ ![]() ,1),点B(﹣2
,1),点B(﹣2 ![]() ,0).
,0).
∵点A与点A1关于直线MN对称,
∴OA1=OA=2,
∴点A1(2,0),
∴A1B=2﹣(﹣2 ![]() )=2+2
)=2+2 ![]() ,
,
∵点A关于直线MN的对称点A1,点B关于直线MN的对称点为B1,
∴AB1=A1B=2+2 ![]() ,OB1=OB=2
,OB1=OB=2 ![]() .
.
在Rt△OB1D中,∠B1OD=∠AOB=30°,
∴B1D= ![]() OB1=
OB1= ![]() .
.
故线段AB1的长为2+2 ![]() ,B1的纵坐标为
,B1的纵坐标为 ![]() .
.
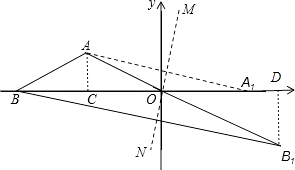
【解析】(1)由点A与点A1关于直线MN对称,可得出∠AOM=∠A1OM,再由等腰三角形的性质可得出∠AOB=30°,通过角的计算即可得出结论;(2)过点A作AC⊥x轴于点C,过点B1作B1D⊥x轴于点D,通过解直角三角形以及等腰三角形的性质可得出点A、B点的坐标,再根据对称的性质即可得出点A1的坐标以及AB1=A1B,在Rt△OB1D中,利用特殊角的三角函数值即可得出B1D的长度,此题得解.
【考点精析】本题主要考查了三角形三边关系和比例的性质的相关知识点,需要掌握三角形两边之和大于第三边;三角形两边之差小于第三边;不符合定理的三条线段,不能组成三角形的三边;基本性质;更比性质(交换比例的内项或外项);反比性质(交换比的前项、后项);等比性质才能正确解答此题.

 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案