Question

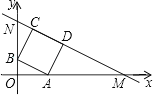
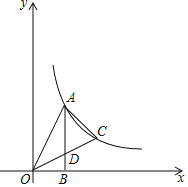
【题目】如图，在平面直角坐标系中，点O为坐标原点，直角三角形AOB的直角顶点B在x轴正半轴上，点A在第一象限，OB＝2，tan∠AOB＝2．

（1）求图象经过点A的反比例函数的解析式；

（2）点C是（1）中反比例函数图象上一点，连接OC交AB于点D，连接AC，若D为OC中点，求△ADC的面积．

Answer 1

【答案】（1）y＝；（2）3

【解析】

（1）依据tan∠AOB＝2，即可得到AB＝2OB＝4，进而得出点A的坐标为(2，4)，利用待定系数法即可得出反比例函数的解析式；

（2）过C作CE⊥x轴于E，则BD∥CE，依据△OBD∽△OEC，即可得到AD＝AB﹣BD＝4﹣1＝3，BE＝2，进而得出S△ACD＝AD×BE＝3．

解：（1）∵直角三角形AOB的直角顶点B在x轴正半轴上，点A在第一象限，OB＝2，tan∠AOB＝2，

∴AB＝2OB＝4，

∴点A的坐标为(2，4)，

设经过点A的反比例函数的解析式为y＝，

则k＝2×4＝8，

∴y＝．

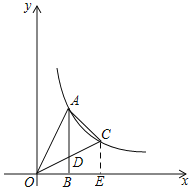
（2）如图所示，过C作CE⊥x轴于E，则BD∥CE，

∴△OBD∽△OEC，

∵D是CO的中点，

∴＝＝＝，

∴OE＝2OB＝4，CE＝2BD＝2，

∴BD＝1，AD＝AB﹣BD＝4﹣1＝3，BE＝2，

∴S△ACD＝AD×BE＝×3×2＝3．