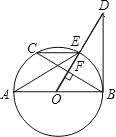
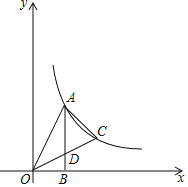
题目内容
【题目】如图，在
中，
，
是
边上的动点(不与点
重合)，将
沿
所在的直线翻折，得到
，连接
，则下列判断：
①当
时，
②当时，
③当
时，
；
④长度的最小值是1．
其中正确的判断是______(填入正确结论的序号)
【答案】①②④
【解析】
①由直角三角形斜边上的中线等于斜边的一半以及折叠的性质，易得
，即可得
;
②由
，可得点
在以
为圆心，
长为半径的圆上，然后在由圆周角定理，求得答案;
③当
时，易得
，再根据相似三角形对应边成比例，求得AP的长;
④易得
，
长度的最小值是1．
解：①∵在
中，
，
∴
，
，
由折叠的性质可得：
∴
，
∴
∴；故①正确；
②∵
，
∴，
∴点在以为圆心，长为半径的圆上，
∵由折叠的性质可得：
，
∴
，
∴
故②正确
③当时，
，
∵
，
∴，
∴
∵在
中，由勾股定理可知
∴
故③错误；
④由轴对称的性质可知：
，
∵
长度固定不变，
∵
∴
的长度有最小值．
有最小值
．故④正确．
故答案为：①②④
练习册系列答案
相关题目
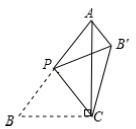
【题目】如图，在
中，点
是线段
上的动点，将线段
绕点逆时针旋转
得到线段
，连接
．若已知
，设
两点间的距离为
两点间的距离为
两点间的距离为
．（若同学们打印的BC的长度如不是
，请同学们重新画图、测量）
小明根据学习函数的经验，分别对
自变量x的变化而变化的规律进行了探究，下面是小明的探究过程，请补充完整：
（1）按照下表中自变量
的值进行取点、画图、测量，分别得到了与的几组对应值，如下表：
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 7.03 | 6.20 | 5.44 | 4.76 | 4.21 | 3.85 | 3.73 | 3.87 | 4.26 |
|
| 5.66 | 4.32 |
| 1.97 | 1.59 | 2.27 | 3.43 | 4.73 |
写出
的值．（保留1位小数）
（2）在同一平面直角坐标系
中，描出补全后的表中各组数值所对应的点
，并画出函数的图象；
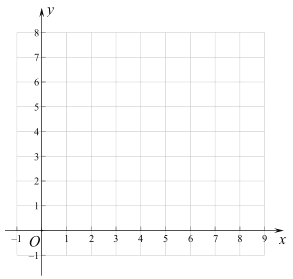
（3）结合函数图像，解决问题：
①当
在线段上时，
的长度约为________
；
②当
为等腰三角形时，的长度约为_______．
