题目内容
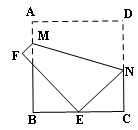
如图,在直角梯形纸片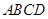 中,
中, ,
,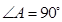 ,
,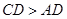 ,将纸片沿过点
,将纸片沿过点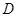 的直线折叠,使点
的直线折叠,使点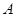 落在边
落在边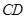 上的点
上的点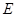 处,折痕为
处,折痕为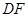 .连接
.连接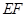 并展开纸片.
并展开纸片.
(1)求证:四边形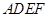 是正方形;
是正方形;
(2)取线段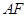 的中点
的中点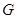 ,连接
,连接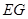 ,如果
,如果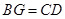 ,试说明四边形
,试说明四边形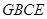 是等腰梯形.
是等腰梯形.
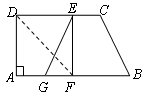
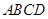 中,
中, ,
,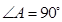 ,
,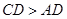 ,将纸片沿过点
,将纸片沿过点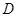 的直线折叠,使点
的直线折叠,使点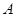 落在边
落在边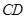 上的点
上的点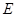 处,折痕为
处,折痕为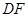 .连接
.连接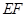 并展开纸片.
并展开纸片.(1)求证:四边形
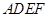 是正方形;
是正方形;(2)取线段
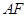 的中点
的中点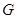 ,连接
,连接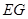 ,如果
,如果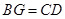 ,试说明四边形
,试说明四边形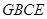 是等腰梯形.
是等腰梯形.
(1)证明见解析;(2)说理见解析.
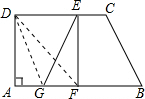
试题分析:(1)由题意知,AD=DE,易证四边形AFED是矩形,所以四边形AFED是正方形,连接DG由于BG与CD平行且相等,所以边形BCDG是平行四边形
(2)由(1)知CB=DG,在正方形AFED中,易证△DAG≌△EFG,所以DG=EG=BC,即四边形GBCE是等腰梯形.
试题解析:(1)∵△DEF由△DAF折叠而得,
∴∠DEF=∠A=90°,DA=DE,
∵AB∥CD,
∴∠ADE=180°-∠A=90°.
∴∠DEF=∠A=∠ADE=90°.
∴四边形ADEF是矩形.
又∵DA=DE,
∴四边形ADEF是正方形.
(2)由折叠及图形特点易得EG与CB不平行,
连接DG,
∵BG∥CD,且BG=CD,
∴四边形BCDG是平行四边形.
∴CB=DG.
∵四边形ADEF是正方形,
∴EF=DA,∠EFG=∠A=90°.
∵G是AF的中点,
∴AG=FG.
在△DAG和△EFG中
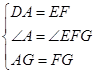 ,
,∴△DAG≌△EFG(SAS).
∴DG=EG.
∴EG=BC.
∴四边形GBCE是等腰梯形.

练习册系列答案
相关题目
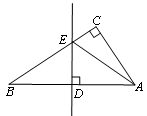
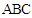 中,
中,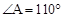 ,则
,则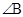 = .
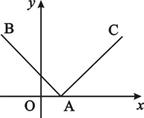
= .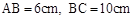 ,E是CD上的点,
,E是CD上的点,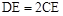 .点P从D点出发,以1cm/s的速度沿DA运动至A点停止.则当△EDP为等腰三角形时,点P的运动时间为 .
.点P从D点出发,以1cm/s的速度沿DA运动至A点停止.则当△EDP为等腰三角形时,点P的运动时间为 .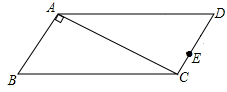
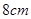 的正方形
的正方形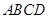 折叠,使点
折叠,使点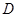 落在
落在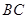 边中点
边中点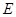 处,点
处,点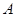 落在点
落在点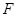 处,折痕为
处,折痕为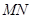 ,则
,则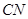 的长为 .
的长为 .