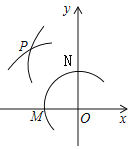��Ŀ����
����Ŀ����֪������x�Ķ��κ���y=x2+bx+c�����㣨��1��0���ͣ�2��6����
��1����b��c��ֵ��
��2������A��n��y1����B��n+1��y2����C��n+2��y3������������κ�����ͼ���ϣ����Ƿ��������n��ʹ![]() �������ڣ������n���������ڣ���˵�����ɣ�
�������ڣ������n���������ڣ���˵�����ɣ�
��3������P�Ƕ��κ���ͼ����y����ಿ���ϵ�һ�����㣬��ֱ��y=��2x��y������ƽ�ƣ��ֱ�x�ᡢy����C��D���㣬����CDΪֱ�DZߵ���PCD����OCD���ƣ���������з���������P�����꣮
���𰸡���1��n=3��n=-5 ��2�� (![]() ,-
,-![]() ) ��(
) ��(![]() ,-
,-![]() )
)
�������������������1�����ô���ϵ�������ɽ�����⣮
��2�����y1��y2��y3����ⷽ�̼��ɽ�����⣬ע�����㼼�ɣ�
��3����DΪֱ�Ƕ���ʱ����ͼ���֪�����ڵ�P��ʹ����PCDΪֱ�������Σ���CΪֱ�Ƕ��㣬CDΪֱ�DZ�ʱ����PE��OC��E������������CD=2PC����PC=2CD��
��ֱ��y=-2x����ƽ��m����λ����ֱ��CD����ʽΪy=-2x-m�������P���꣨��m��ʾ�������������߽���ʽ���ɽ�����⣮
�����������1���ѣ�-1��0���ͣ�2��6������y=x2+bx+c�У�
��![]() �����
�����![]() ��
��
��b=1��c=0��
��2��������y1=n2+n��y2=��n+1��2+��n+1����y3=��n+2��2+��n+2����
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
������n2+3n-10=0��
���n=2��-5��
��������n=2��-5�Ƿ�ʽ���̵Ľ⣮
��3����DΪֱ�Ƕ���ʱ����ͼ���֪�����ڵ�P��ʹ����PCDΪֱ�������Σ���CΪֱ�Ƕ��㣬CDΪֱ�DZ�ʱ����PE��OC��E��

��ֱ��y=-2x����ƽ��m����λ����ֱ��CD����ʽΪy=-2x-m��
���D���꣨0��-m������C���꣨-![]() ��0����
��0����
��OD=m��OC=![]() ��
��
��OD=20C��
�ߡ�PCD����OCD���ƣ�
��CD=2PC��PC=2CD��
�ٵ�CD=2PCʱ��
�ߡ�PCD=90����
���PCE+��DCO=90������DCO+��CDO=90����
���PCE=��CDO��
�ߡ�PEC=��COD=90����
���COD�ס�PEC��
��![]() ��
��
��EC=![]() ��PE=
��PE=![]() ��
��
���P���꣨-m��-![]() ��������y=x2+x��
��������y=x2+x��
��-![]() =m2-m�����m=
=m2-m�����m=![]() ��0������
��0������
���P���꣨-![]() ��-
��-![]() ����
����
��PC=2CDʱ����![]() ��
��
��EC=2m��PE=m��
���P���꣨-![]() m��-m��������y=x2+x��
m��-m��������y=x2+x��
��-m=![]() m2-
m2-![]() m��
m��
���m=![]() �ͣ�0��������
�ͣ�0��������
���P���꣨-![]() ��-
��-![]() ����
����

 Ʒѧ˫�ž�ϵ�д�
Ʒѧ˫�ž�ϵ�д� Сѧ��ĩ���100��ϵ�д�
Сѧ��ĩ���100��ϵ�д� ��ĩ��ϰ���ϵ�д�
��ĩ��ϰ���ϵ�д�