��Ŀ����
����Ŀ����ͼ1��������y=ax2+bx+2��x�ύ��A��B���㣬��y�ύ�ڵ�C��AB=4������OBDC�ı�CD=1���ӳ�DC���������ڵ�E��
��1���������ߵĽ���ʽ��
��2����ͼ2����P��ֱ��EO�Ϸ��������ϵ�һ�����㣬����P��y���ƽ���߽�ֱ��EO�ڵ�G����PH��EO������ΪH����PH�ij�Ϊl����P�ĺ�����Ϊm����l��m�ĺ�����ϵʽ������д��m��ȡֵ��Χ���������l�����ֵ��
��3�������N�������߶Գ����ϵ�һ�㣬���������Ƿ���ڵ�M��ʹ����M��A��C��NΪ������ı�����ƽ���ı��Σ������ڣ�ֱ��д���������������ĵ�M�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺�߾���OBDC�ı�CD=1��
��OB=1��
��AB=4��
��OA=3��
��A����3��0����B��1��0����
��A��B����������������߽���ʽ�ɵ� ![]() �����
�����  ��
��
�������߽���ʽΪy=�� ![]() x2��
x2�� ![]() x+2��
x+2��
��2��
�⣺��y=�� ![]() x2��
x2�� ![]() x+2�У���y=2�ɵ�2=��
x+2�У���y=2�ɵ�2=�� ![]() x2��
x2�� ![]() x+2�����x=0��x=��2��
x+2�����x=0��x=��2��
��E����2��2����
��ֱ��OE����ʽΪy=��x��
������ɵ�P��m���� ![]() m2��
m2�� ![]() m+2����
m+2����
��PG��y�ᣬ
��G��m����m����
��P��ֱ��OE���Ϸ���
��PG=�� ![]() m2��
m2�� ![]() m+2������m��=��
m+2������m��=�� ![]() m2��
m2�� ![]() m+2=��
m+2=�� ![]() ��m+
��m+ ![]() ��2+
��2+ ![]() ��
��
��ֱ��OE����ʽΪy=��x��
���PGH=��COE=45�㣬
��l= ![]() PG=
PG= ![]() [��
[�� ![]() ��m+
��m+ ![]() ��2+
��2+ ![]() ]=��
]=�� ![]() ��m+
��m+ ![]() ��2+
��2+ ![]() ��
��
�൱m=�� ![]() ʱ��l�����ֵ�����ֵΪ
ʱ��l�����ֵ�����ֵΪ ![]() ��
��
��3��
�⣺�ٵ�ACΪƽ���ı��εı�ʱ������MN��AC����MN=AC����ͼ����M���Գ���Ĵ��ߣ�����ΪF����AC���Գ����ڵ�L��

���ALF=��ACO=��FNM��
�ڡ�MFN�͡�AOC��
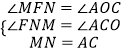
���MFN�ա�AOC��AAS����
��MF=AO=3��
���M���Գ���ľ���Ϊ3��
��y=�� ![]() x2��
x2�� ![]() x+2��
x+2��
�������߶Գ���Ϊx=��1��
��M��������x��y������|x+1|=3�����x=2��x=��4��
��x=2ʱ��y=�� ![]() ����x=��4ʱ��y=
����x=��4ʱ��y= ![]() ��
��
��M��������2���� ![]() ����4����
����4���� ![]() ����
����
�ڵ�ACΪ�Խ���ʱ����AC���е�ΪK��
��A����3��0����C��0��2����
��K���� ![]() ��1����
��1����
�ߵ�N�ڶԳ����ϣ�
���N�ĺ�����Ϊ��1��
��M�������Ϊx��
��x+����1��=2������ ![]() ��=��3�����x=��2����ʱy=2��
��=��3�����x=��2����ʱy=2��
��M����2��2����
���Ͽ�֪��M������Ϊ��2���� ![]() ����4����
����4���� ![]() ����2��2����
����2��2����
����������1�������������A��B�����꣬���ô���ϵ��������������߽���ʽ����2���������E�����꣬�Ӷ������ֱ��OE����ʽ����֪��PGH=45�㣬��m�ɱ�ʾ��PG�ij����Ӷ��ɱ�ʾ��l�ij��������ö��κ��������ʿ���������ֵ����3����ACΪ�ߺ�ACΪ�Խ��ߣ���ACΪ��ʱ����M���Գ���Ĵ��ߣ�����ΪF�����֤�á�MFN�ա�AOC�������M���Գ���ľ��룬�Ӷ������M��ĺ����꣬�����M������ꣻ��ACΪ�Խ���ʱ����AC���е�ΪK�������K�ĺ����꣬�Ӷ������M�ĺ����꣬���������߽���ʽ�����M�����꣮
�����㾫�����������⣬������Ҫ�˽���κ���������(�����ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С)��

 �¿α�ͬ��ѵ��ϵ�д�
�¿α�ͬ��ѵ��ϵ�д� һ����ʦ����Ӧ����������һ��ȫϵ�д�
һ����ʦ����Ӧ����������һ��ȫϵ�д� Сѧѧϰ�ð���ϵ�д�
Сѧѧϰ�ð���ϵ�д�����Ŀ��������ڼ�ijˮ����ֳ��Ϊ��Ӧ�г�����������20��ʱ�䣬����ÿ�콵��ˮλ�Լ��ٲ��̳ɱ��İ취����ˮ����ij��������в������ۣ���x�죨1��x��20��xΪ�������IJ��������۵������Ϣ���£�
�������۵��ۣ�Ԫ/kg�� | 20 |
��λ���̳ɱ���Ԫ/kg�� | 5�� |
��������kg�� | 950��10x |
�ٶ�����ֳ��ÿ�첶�̺����۵�����û����ʧ�������ڵ���ȫ���۳���
��1�����x�������y��Ԫ����x���죩֮��ĺ�����ϵʽ������������=�����۶�ղ��̳ɱ���
��2���ڵڼ���yȡ�����ֵ�����ֵ�Ƕ��٣�



