题目内容
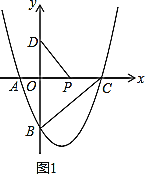
【题目】在平面直角坐标系xOy中，点A（a，0）为x轴上一动点，点M（1，﹣1）、点N（3，﹣4），连接AM、MN，点N关于直线AM的对称点为N′．
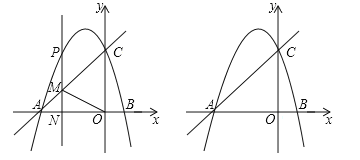
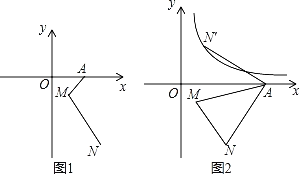
（1）若a＝2，在图1中画出线段MN关于直线AM的对称图形MN′（保留作图痕迹），直接写出点N′的坐标 ；
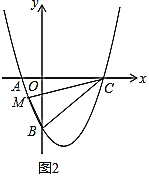
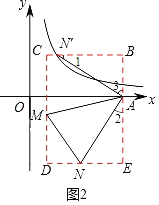
（2）若a＞0，连接AN、AN′，当点A运动到∠N′AN＝90°时，点N′恰好在双曲线y＝
上（如图2），求k的值；
（3）点A在x轴上运动，若∠N′MN＝90°，此时a的值为 ．
【答案】（1）（﹣2，1）；（2）20；（3）﹣4或
【解析】
（1）根据要求画出图形，利用图象法解决问题即可．
（2）如图2，过A，M分别作y轴平行线BE，CD，过N，N′分别作x轴平行线，交BE，CD于点D，B，C．利用全等三角形的性质解决问题即可．
（3）画出图形，利用图象法解决问题．
解：(1)作图如图1所示，N′（﹣2，1）．
故答案为（﹣2，1）．
(2)如图2，过A，M分别作y轴平行线BE，CD，过N，N′分别作x轴平行线，交BE，CD于点D，B，C．
∴∠B＝∠E＝∠D＝∠C＝90°，
∴∠1+∠3＝90°，
∵∠N’AN＝90°，
∴∠2+∠3＝90°，
∴∠1＝∠2
又AN′＝AN，
∴△ABN≌△NEA（AAS），
∴BA＝EN，BN＝EA
∵A（a，0），M（1，﹣1），N（3，﹣4），
∴BA＝EN＝a﹣3，BN′＝EA＝4，DM＝2，DM＝3，
N′（a﹣4，a﹣3），由轴对称性质可知MN′＝MN＝
，
∴NC＝a﹣4﹣1＝a＝5，CM＝a＝3﹣（﹣1）＝a﹣2
CN2+CM2＝MN2＝13，
∴（a﹣5）2+（a﹣2）2＝13，
∴a2﹣7a﹣8＝0，
∴k＝（a﹣4）（a﹣3）＝a2﹣7a+12＝（a2﹣7a﹣8）+20＝20．
故答案为：20；
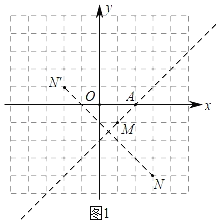
(3)如下图中，
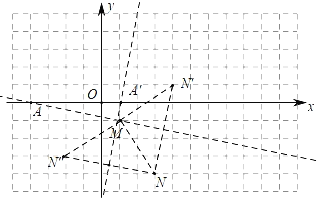
将线段MN绕点M逆时针旋转90°得到N′（4，1），作线段NN′的垂直平分线交x轴于A，
∴直线NN′的解析式为y＝5x﹣19，
∴线段NN′的中垂线的解析式为
，可得A（﹣4，0）．
将线段MN绕点M顺时针旋转90°得到N″（﹣2，﹣3），作线段N″N′的垂直平分线交x轴于A′，同法可得直线y＝5x﹣6，
∴A′（，0）．
∴a＝﹣4或．
故答案为﹣4或．
