题目内容
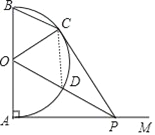
【题目】如图,AB是半圆O的直径,射线AM⊥AB,点P在AM上,连接OP交半圆O于点D,PC切半圆O于点C,连接BC,OC.
(1)求证:△OAP≌△OCP;
(2)若半圆O的半径等于2,填空:
①当AP= 时,四边形OAPC是正方形;
②当AP= 时,四边形BODC是菱形.

【答案】(1)证明见解析;(2)①2;②2![]() .
.
【解析】试题分析:(1)根据切线的性质,可以得到OP⊥AC,然后利用“HL”证明:△OAP≌△OCP;
(2)①根据正方形的性质可以得到AP的长;
②先利用菱形的性质得到△OBC为等边三角形,则∠B=60°,所以∠AOP=60°,然后在Rt△OAP中利用正切的定义求AP即可.
试题解析:(1)∵PC切半圆O于点C,∴OC⊥PC,
∵AM⊥AB,∴∠OAP=90°,
在Rt△OAP和Rt△OCP中![]() ,∴Rt△OAP≌Rt△OCP;
,∴Rt△OAP≌Rt△OCP;
(2)①∵Rt△OAP≌Rt△OCP,∴PA=PC,
而OA=OC,∴当AO=AP时,四边形OAPC为菱形,
而∠OAP=90°,∴四边形OAPC是正方形,此时AP=OA=2;
②∵四边形BODC是菱形,∴OB=OD=CD=BC,BC∥OD,∴△OBC为等边三角形,
∴∠B=60°,∴∠AOP=60°,
在Rt△OAP中,∵tan∠AOP=![]() ,∴AP=2tan60°=2
,∴AP=2tan60°=2![]() ,
,
即AP=2![]() 时,四边形BODC是菱形.
时,四边形BODC是菱形.
故答案为2,2![]() .
.

 互动英语系列答案
互动英语系列答案【题目】为了强化司机的交通安全意识,我市利用交通安全宣传月对司机进行了交通安全知识问卷调查.关于酒驾设计了如下调查问卷:
克服酒驾﹣﹣你认为哪种方式最好?(单选) |
A加大宣传力度,增强司机的守法意识. B在汽车上张贴温馨提示:“请勿酒驾”. C司机上岗前签“拒接酒驾”保证书. D加大检查力度,严厉打击酒驾. E查出酒驾追究一同就餐人的连带责任. |
随机抽取部分问卷,整理并制作了如下统计图:

根据上述信息,解答下列问题:
(1)本次调查的样本容量是多少?
(2)补全条形图,并计算B选项所对应扇形圆心角的度数;
(3)若我市有3000名司机参与本次活动,则支持D选项的司机大约有多少人?