题目内容
【题目】已知二次函数y=x2﹣(a﹣1)x+a﹣2,其中a是常数. 
(1)求证:不论a为何值,该二次函数的图象与x轴一定有公共点;
(2)当a=4时,该二次函数的图象顶点为A,与x轴交于B,D两点,与y轴交于C点,求四边形ABCD的面积.
【答案】
(1)证明:y=x2﹣(a﹣1)x+a﹣2.
因为[﹣(a﹣1)]2﹣4(a﹣2)=(a﹣3)2≥0.
所以,方程x2﹣(a﹣1)x+a﹣2=0有实数根.
所以,不论a为何值,该函数的图象与x轴总有公共点;
(2)解:由题可知:当a=4时,y=x2﹣3x+2,
因为y=x2﹣3x+2=(x﹣ ![]() )2﹣
)2﹣ ![]() ,所以A(
,所以A( ![]() ,﹣
,﹣ ![]() ),
),
当y=0时,x2﹣3x+2=0,解得x1=1,x2=2,所以B(1,0),D(2,0),
当x=0时,y=2,所以C(0,2),
所以S四边形ABCD=S△ABD+S△BDC= ![]() +1=
+1= ![]() .
.
【解析】(1)利用根的判别式符号进行证明;(2)由抛物线解析式求得点B、C、D的坐标,然后利用分割法来求四边形ABCD的面积.
【考点精析】通过灵活运用抛物线与坐标轴的交点,掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.即可以解答此题.

【题目】某学校为了了解本校学生采用何种方式上网查找所需要的学习资源,随机抽取部分学生了解情况,并将统计结果绘制成频数分布表及频数分布直方图. 上网查找学习资源方式频数分布表
查找方式 | 频数 | 频率 |
搜索引擎 | 16 | 32% |
专题网站 | 15 | a |
在线网校 | 4 | 8% |
试题题库 | 10 | 20% |
其他 | b | 10% |
(1)频数分布表中a,b的值:a=;b=;
(2)补全频数分布直方图; 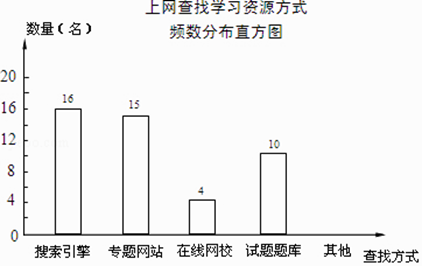
(3)若全校有1000名学生,估计该校利用搜索引擎上网查找学习资源的学生有多少名?
【题目】我国古籍《周髀算经》中早有记载“勾三股四弦五”,下面我们来探究两类特殊的勾股数.通过观察完成下面两个表格中的空格(以下a、b、c为Rt△ABC的三边,且a<b<c):
表一 表二
a | b | c | a | b | c | |
3 | 4 | 5 | 6 | 8 | 10 | |
5 | 12 | 13 | 8 | 15 | 17 | |
7 | 24 | 25 | 10 | 24 | 26 | |
9 | 41 | 12 | 37 |
(1)仔细观察,表一中a为大于1的奇数,此时b、c的数量关系是_____________,
a、b、c之间的数量关系是_________________________;
(2)仔细观察,表二中a为大于4的偶数,此时b、c的数量关系是_____________,
a、b、c之间的数量关系是_________________________;
(3)我们还发现,表一中的三边长“3,4,5”与表二中的“6,8,10”成倍数关系,表一中的“5,12,13”与表二中的“10,24,26”恰好也成倍数关系……请直接利用这一规律计算:在Rt△ABC中,当![]() ,
,![]() 时,斜边c的值.
时,斜边c的值.