Question

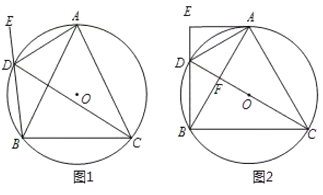
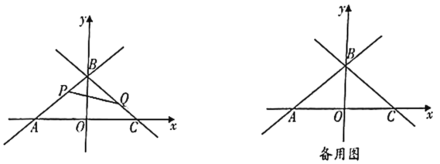
【题目】如图①，△ABC是等腰直角三角形，在两腰AB、AC外侧作两个等边三角形ABD和ACE，AM和AN分别是等边三角形ABD和ACE的角平分线，连接CM、BN，CM与AB交于点P．

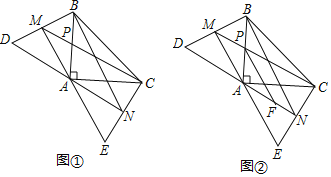
（1）求证：CM＝BN；

（2）如图②，点F为角平分线AN上一点，且∠CPF＝30°，求证：△APF∽△AMC；

（3）在（2）的条件下，求的值．

Answer 1

【答案】（1）见解析（2）见解析（3）

【解析】

（1）根据△ABC是等腰直角三角形，AM和AN分别是等边三角形ABD和ACE的角平分线，即可得到AB＝AC，∠BAC＝90°，∠BAM＝∠CAN＝30°，AM＝AN，进而得出△BAN≌△CAM，进而得到CM＝BN；

（2）依据∠APF＝∠AMC，∠MAC＝∠PAF＝120°，即可判定△APF∽△AMC；

（3）连接CF，依据A，F，C，P四点共圆，可得∠AFP＋∠CFN＝90°，根据∠CFN＋∠FCN＝90°，可得∠FCN＝∠AFP＝∠ACM．再根据∠FNC＝∠PAC＝90°，可得△PAC∽△FNC，进而得出＝2①；根据△APF∽△AMC，可得②，联立①②可得，进而得到．

（1）∵△ABC是等腰直角三角形，AM和AN分别是等边三角形ABD和ACE的角平分线，

∴AB＝AC，∠BAC＝90°，∠BAM＝∠CAN＝30°，AM＝AN，

∴∠BAN＝∠CAM＝120°，

∴△BAN≌△CAM，

∴CM＝BN；

（2）∵∠APF＝∠APC∠CPF＝∠APC30°，∠AMC＝∠APC∠MAB＝∠APC30°，

∴∠APF＝∠AMC，

又∵∠MAC＝∠PAF＝120°，

∴△APF∽△AMC；

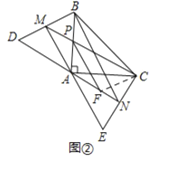
（3）如图②，连接CF，

∵△APF∽△AMC，

∴∠AFP＝∠ACM，

∴A，F，C，P四点共圆，

∴∠PFC＝∠PAC＝90°，

∴∠AFP＋∠CFN＝90°，

∵∠CFN＋∠FCN＝90°，

∴∠FCN＝∠AFP＝∠ACM．

又∵∠FNC＝∠PAC＝90°．

∴△PAC∽△FNC，

∴＝=2①；

∵△APF∽△AMC，

∴②，

由①可得，FN＝AP；由②可得，AF＝AP，

∴．

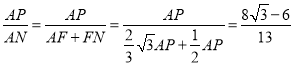∵△APF∽△AMC，

∴，AM＝AN，

∴．