��Ŀ����
����Ŀ��Сӱ��С����ɽ���棬Сӱ�����³���С�����У�������Լ��ɽ�����³��յ��ϣ���֪С�����ߵ��³��յ��·�����³���ɽ������·����2����Сӱ��С��������50min�ų����³����³���ƽ���ٶ�Ϊ180m/min����С������xmin�����ߵ�·��Ϊym��ͼ�е����߱�ʾС�����������߹�����y��x�ĺ�����ϵ��
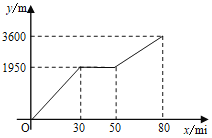
��1��С�����ߵ���·����______m����;����Ϣ��______min����Ϣ��������ߵ��ٶ�Ϊ______m/min��
��2����![]() ʱ����y��x�ĺ�����ϵʽ��
ʱ����y��x�ĺ�����ϵʽ��
��3����Сӱ�����³��յ�ʱ��С�����³��յ��·���Ƕ��٣�
���𰸡���1��3600��20��55����2��y=55x-800����3����Сӱ�����³��յ�ʱ��С�����³��յ��·����1100m��
��������
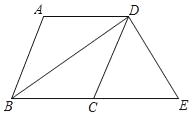
��1���۲캯��ͼ���ҳ�С�����ߵ���·�̼�;����Ϣ��ʱ�䣬�������ٶ�=·����ʱ������С����Ϣ��������ߵ��ٶȣ�
��2���۲�ͼ���ҳ�������꣬���ô���ϵ���������������50��x��80ʱ��y��x�ĺ�����ϵʽ��
��3������Сӱ�����յ����õ�ʱ��=�����³�����·�����³���ƽ���ٶȿ����Сӱ�����յ����õ�ʱ�䣬�������50�����Сӱ�����յ�ʱС������ʱ�䣬������С�����³��յ��·��=С����Ϣ��������ߵ��ٶ����������յ��ʱ��-Сӱ�����յ�ʱС������ʱ�䣩����������ۣ�
�⣺��1���۲캯��ͼ��֪��С�����ߵ���·����3600m��
С��;����Ϣ��ʱ��Ϊ��50-30=20��min����
��Ϣ��������ߵ��ٶ�Ϊ����3600-1950������80-50��=55��m/min����
�ʴ�Ϊ��3600��20��55��
��2���赱50��x��80ʱ��y��x�ĺ�����ϵʽΪy=kx+b��k��0����
��ͼ��֪���㣨50��1950����㣨80��3600����ֱ���ϣ�
��![]() ����ã�
����ã�![]() ��
��
����50��x��80ʱ��y��x�ĺ�����ϵʽΪy=55x-800��
��3��Сӱ�����յ����õ�ʱ��Ϊ1800��180=10�����ӣ���
��Сӱ�����յ�ʱС������ʱ50+10=60�����ӣ���
��С�����³��յ��·��Ϊ55����80-60��=1100��m����
�𣺵�Сӱ�����³��յ�ʱ��С�����³��յ��·����1100m��

 ���ſ����ϵ�д�
���ſ����ϵ�д� ���Ŀ����ϵ�д�
���Ŀ����ϵ�д� ������ӱ������ͯ������ϵ�д�
������ӱ������ͯ������ϵ�д�����Ŀ������ij�и���ס������˰���չ���ϸ�ߵ�ס��������������۴ﵽ��һ����������Ʒס��������۵�2����ʼ���շ���˰��2������2������3����ס��������˰��˰��Ϊ0.5%��3������3������4���ģ�����˰˰��Ϊ1%��4������4�������Ϸ���˰˰��Ϊ1.2%��ϸ��涨����ڶ��꿪ʼ������˰������������±���
��˰��� | ��һ����������Ʒ���ɽ������������ |
2016�� | 2015�����6600Ԫ/m2 |
2017�� | 2016�����7000Ԫm2 |
2018�� | 2017�����7800Ԫm2 |
����ס������˰Ӧ��˰��ļ��㹫ʽ����Ӧ��˰���������������������������˰�ʣ����磺2015�꽨������ɽ�����Ϊ20000Ԫ/m2��һ��100m2��Ʒ����2016�꿪ʼ��һ�ν�����˰����6600��3��20000��6600��4����2016��Ӧ������˰100��20000��1%��20000Ԫ����7000��2��20000��7000��3����2017��Ӧ������˰��100��20000��0.5%��10000Ԫ��
��1������2016������һ�������Ϊ150m2�Ĵ�ƽ�㻧�ͣ�2017�꽻��12000Ԫ�ķ���˰������������ķ��ӵĽ�������ɽ������Ƕ���Ԫ/m2��
��2��2017���������˺�����ͬ���͵�һ����������������������ǣ�����ͨ�����㷢�֣���2017�깺��������2018������ɵķ���˰֮�ͱ�����2016�깺��������2017��2018��������ɵķ���˰֮�Ͷ��121.2��Ԫ����2017��������ʱ������������Ƕ���Ԫ/m2��