题目内容
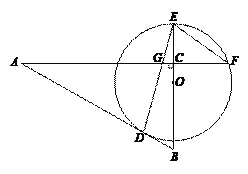
【题目】三角形中,顶角等于![]() 的等腰三角形称为黄金三角形,如图
的等腰三角形称为黄金三角形,如图![]() ,在
,在![]() 中,已知:
中,已知:![]() ,且
,且![]() .
.
![]() 在图
在图![]() 中,用尺规作
中,用尺规作![]() 的垂直平分线交
的垂直平分线交![]() 于
于![]() ,并连接
,并连接![]() (保留作图痕迹,不写作法);
(保留作图痕迹,不写作法);
![]() 是不是黄金三角形?如果是,请给出证明;如果不是,请说明理由;
是不是黄金三角形?如果是,请给出证明;如果不是,请说明理由;
![]() 设
设![]() ,试求
,试求![]() 的值;
的值;
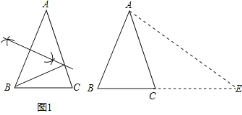
![]() 如图
如图![]() ,在
,在![]() 中,已知
中,已知![]() ,
,![]() ,且
,且![]() ,请直接写出
,请直接写出![]() 的值.
的值.

【答案】(1)详见解析;(2)详见解析;(3)![]() ;(4)
;(4)![]() .
.
【解析】
(1)根据作线段垂直平分线的方法作图即可;(2)分别求得△BCD各个角的度数,根据黄金三角形的定义即可解答;(3)通过证明△BDC∽△ABC,根据相似三角形的性质求解即可;(4)延长![]() 到
到![]() ,使
,使![]() ,连接
,连接![]() ,证明
,证明![]() ,可得
,可得![]() .根据(3)可得
.根据(3)可得![]() ,
,![]() ,由此即可求得
,由此即可求得![]() 的值.
的值.
![]() 如图所示;
如图所示;
![]() 是黄金三角形.
是黄金三角形.
证明如下:∵点![]() 在
在![]() 的垂直平分线上,
的垂直平分线上,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 是黄金三角形.
是黄金三角形.
![]() 设
设![]() ,
,![]() ,
,
由![]() 知,
知,![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
整理,得![]() ,
,
解得![]() .
.
因为![]() 、
、![]() 均为正数,所以
均为正数,所以![]() .
.
![]() .
.
理由:延长![]() 到
到![]() ,使
,使![]() ,连接
,连接![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
由![]() 知,
知,
∴![]() ,
,![]() ,
,
∴![]() .
.

练习册系列答案
相关题目