题目内容
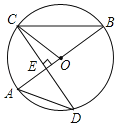
【题目】如图,在直角坐标平面xOy内,点A(6,0)、C(﹣4,0),过点A作直线AB,交y轴的正半轴于点B,且AB=10,点P是直线AB上的一个动点.
(1)求点B的坐标和直线AB的表达式;
(2)若以A、P、C为顶点的三角形与△AOB相似,求点P的坐标.

【答案】(1)直线AB的表达式为y=﹣![]() x+8;(2)点P的坐标为(﹣4,
x+8;(2)点P的坐标为(﹣4,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
(1)由点A的坐标可得出OA的长,利用勾股定理可求出OB的长,结合点B在y轴正半轴上即可得出点B的坐标,由点A,B的坐标,再利用待定系数法即可求出直线AB的解析式;
(2)分△AOB∽△ACP和△AOB∽△APC两种情况考虑:①当△AOB∽△ACP时,∠ACP1=∠AOB=90°,利用一次函数图象上点的坐标特征可求出点P1的坐标;②当△AOB∽△APC时,设点P2的坐标为(m,﹣![]() m+8),利用相似三角形的性质可求出CP2的长,结合点C的坐标可得出关于m的方程,解之即可得出点P2的坐标.综上,此题得解.
m+8),利用相似三角形的性质可求出CP2的长,结合点C的坐标可得出关于m的方程,解之即可得出点P2的坐标.综上,此题得解.
解:(1)∵点A的坐标为(6,0),
∴OA=6,
∴OB=![]() =8.
=8.
∵点B在y轴的正半轴,
∴点B的坐标为(0,8).
设直线AB的表达式为y=kx+b(k≠0),
将A(6,0),B(0,8)代入y=kx+b,得:![]() ,
,
解得: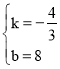 ,
,
∴直线AB的表达式为y=﹣![]() x+8.
x+8.
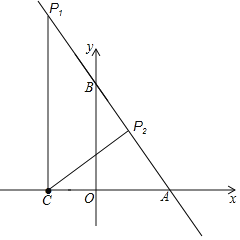
(2)分两种情况考虑,如图所示.
①当△AOB∽△ACP时,∠ACP1=∠AOB=90°,
当x=﹣4时,y=﹣![]() x+8=
x+8=![]() ,
,
∴点P1的坐标为(﹣4,![]() );
);
②当△AOB∽△APC时,设点P2的坐标为(m,﹣![]() m+8).
m+8).
∵点A的坐标为(6,0),点C的坐标为(﹣4,0),
∴AC=10.
∵△AOB∽△AP2C,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴CP2=8,
∴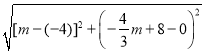 =8,
=8,
整理,得:(![]() m﹣4)2=0,
m﹣4)2=0,
解得:m=![]() ,
,
∴点P2的坐标为(![]() ,
,![]() ).
).
综上所述:点P的坐标为(﹣4,![]() )或(
)或(![]() ,
,![]() ).
).

 活力课时同步练习册系列答案
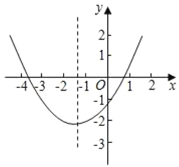
活力课时同步练习册系列答案【题目】已知二次函数的解析式是y=x2﹣2x﹣3.
(1)与y轴的交点坐标是 ,顶点坐标是 .
(2)在坐标系中利用描点法画出此抛物线;
x | … | … | |||||
y | … | … |
(3)结合图象回答:当﹣2<x<2时,函数值y的取值范围是 .