题目内容
如图,在△ABC中,D、E分别是AB、AC上的点,且DE∥BC,若AD=5,DB=3,DE=4,则BC等于
A. B.
B. C.
C. D.
D.
D.
解析试题分析:由AD=5,BD=3,即可求得AB=8,又由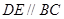 得:△ADE∽△ABC,根据相似三角形的对应边成比例,即可得
得:△ADE∽△ABC,根据相似三角形的对应边成比例,即可得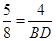 ,则可求得
,则可求得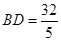 .故选D.
.故选D.
考点:相似三角形的性质.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
如图,△ABC为等腰直角三角形,∠BAC=90°,BC=2,E为AB上任意一动点,以CE为斜边作等腰Rt△CDE,连接AD,下列说法:
①∠BCE=∠ACD;②AC⊥ED;③△AED∽△ECB;④AD∥BC;⑤四边形ABCD的面积有最大值,且最大值为 .其中,正确的结论是 。
.其中,正确的结论是 。
| A.①②④ | B.①③⑤ | C.②③④ | D.①④⑤ |

若△ABC∽△A′B′C′,∠A=40°,∠B=60°,则∠C′等于 ( )
| A.20°; | B.40°; | C.60°; | D.80°. |
如图,在△ABC中,若DE∥BC,AD=5,BD=10,DE=4,则BC的值为( )
| A.8 | B.9 | C.10 | D.12 |
△ABC∽△A′B′C′,如果∠A=55°,∠B=100°,则∠C′的度数等于( )
| A.55° | B.100° | C.25° | D.30° |
如图,在△ 中,
中, 为
为 边上一点,∠
边上一点,∠ ∠
∠ ,
, ,
, ,则
,则 的长为( )
的长为( )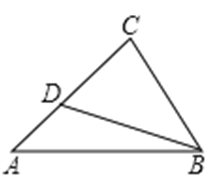
| A.1 | B.4 | C.3 | D.2 |




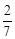

 B.
B. C.
C. D.
D.