Question

【题目】中，，，的半径长是，当时，与直线的位置关系是________；当时，与直线的位置关系是________．

Answer 1

【答案】相交 相切

【解析】

据题意画出相应的图形，然后过C作CD与AB垂直，垂足为D，在直角三角形ACD中，由30°角所对的直角边等于斜边的一半，由斜边AB的长和面积定值求出CD的长，即为圆心到直线的距离，小于圆C的半径，可得圆C与直线AB相交；当∠A=45°时，求出CD的长和圆的半径2比较大小即可．

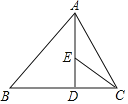
根据题意画出图形，如图所示：

当∠A=30°，

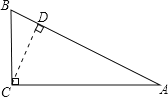
过C作CD⊥AB，交AB于点D，

在Rt△ACD中，∵AB=4，∠A=30°，

∴BC=AB=2，

∴AC==2，

∴CD=AC=，

又∵圆C的半径为2，则＜2，

∴CD＜R，

∴则⊙C与AB的位置关系是相交，

故答案为：相交；

当∠A=45°时，

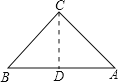
过C作CD⊥AB，交AB于点D，

在Rt△ACD中，∵AB=4，∠A=45°，

∴AB=AC，

∴CD=AB=2，

又∵圆C的半径为2，则CD=R，

∴则⊙C与AB的位置关系是相切．

故答案为：相切．