题目内容
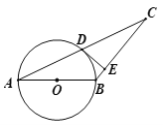
【题目】如图,已知平行四边形OABC的三个顶点A、B、C在以O为圆心的半圆上,过点C作CD⊥AB,分别交AB、AO的延长线于点D、E,AE交半圆O于点F,连接CF.
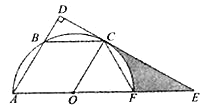
(1)判断直线DE与半圆O的位置关系,并说明理由;
(2)若半圆O的半径为12,求涂色部分的周长.
【答案】(1)相切,理由见解析;(2)![]() .
.
【解析】
(1)结论:DE是⊙O的切线.首先证明△ABO,△BCO都是等边三角形,再证明四边形BDCG是矩形,即可解决问题;
(2)求出EC、EF、弧长CF即可解决问题.
(1)结论:DE是⊙O的切线,
理由:∵四边形OABC是平行四边形,
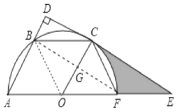
又∵OA=OC,
∴四边形OABC是菱形,
∴OA=OB=AB=OC=BC,
∴△ABO,△BCO都是等边三角形,
∴∠AOB=∠BOC=∠COF=60°,
∵OB=OF,
∴OG⊥BF,
∵AF是直径,CD⊥AD,
∴∠ABF=∠DBG=∠D=∠BGC=90°,
∴四边形BDCG是矩形,
∴∠OCD=90°,
∴DE是⊙O的切线.
(2)在Rt△OCE中,∵OC=12,∠COE=60°,∠OCE=90°,
∴OE=2OC=24,EC=12![]() ,
,
∵OF=12,
∴EF=12,
∴弧CF的长=![]() =4π,
=4π,
∴阴影部分的周长为4π+12+12![]() .
.

练习册系列答案
相关题目