Question

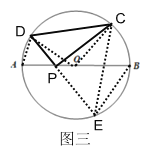
【题目】如图，⊙O的直径AB=20，P是AB上（不与点A，B重合）的任一点，点C，D为⊙O上的两点，若∠APD=∠BPC，则称∠DPC为直径AB的“回旋角”，利用圆的对称性可知：“回旋角”∠DPC的度数与弧CD的度数相等.

（1）若∠DPC为直径AB的“回旋角”，且∠DPC=100°，求∠APD的大小；

（2）若直径AB的“回旋角”为90°，且△PCD的周长为，求AP的长.

Answer 1

【答案】（1）40°；（2）或

【解析】

（1）根据“回旋角”的定义可得∠APD=∠BPC，结合∠DPC=100°可求∠APD的大小；

（2）如图三，延长DP交⊙O于点E，连结CE、OC、OD，根据勾股定理求出，可得PC+PD=16，然后在Rt△DPC中，利用勾股定理构造方程求出PD=2，PC=14，或PD=14，PC=2，然后分情况讨论，利用△DPA∽△BPE列出比例式，分别求出相应的AP的长即可.

解：（1）∵∠DPC为直径AB的“回旋角”，

∴∠APD=∠BPC，

又∵∠DPC=100°，

∴∠APD+∠BPC=180°-100°=80°，

∴∠APD=40°；

（2）如图三，∠DPC=90°，延长DP交⊙O于点E，连结CE、OC、OD，

∵“回旋角”∠DPC的度数与弧CD的度数相等，

∴∠DOC=90°，

∴，

∵△PCD的周长为，

∴PC+PD=16，

设PD=x，则PC=（16-x），

在Rt△DPC中，PD2+PC2=CD2，即，

解得：x1=2，x2=14，

∴PD=2，PC=14，或PD=14，PC=2，

∵∠DOC=90°，∠DPC=90°，

∴∠DEC=45°，

∴PE=PC，

①当PD=2，PE=PC=14时，连结AD，BE，

∵∠DAB=∠DEB，∠DPA=∠BPE，

∴△DPA∽△BPE，

∴，即，

解得：（已舍去不合题意的值），

②当PD=14，PE=PC=2时，

同理可得：.

综上，AP的长为：或.